Lecture 09. Expectation, Indicator Random Variables, Linearity

이 포스팅은 Harvard에서 진행된 Joe Blitzstein의 Statics 110 강좌를 기반으로 작성되었습니다.

• 강의 및 자료 링크

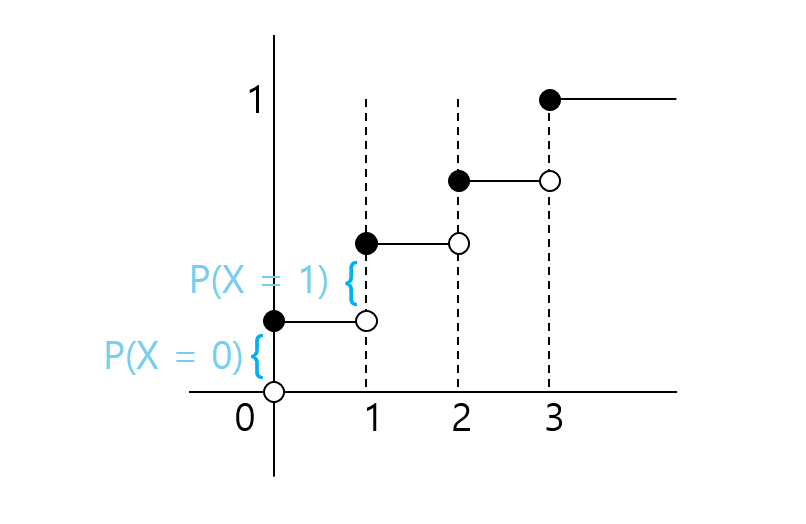
CDF (누적분포함수)

\[F(X) = P(X \leqslant x) \text{, as a function of real } x\]

• $x=0$일 때 점의 위치가 $P(x=0)$
• 각 위치에서의 jump 간격이 각 값일 때의 확률이 된다.

[Example] Find $P(1 < X \leqslant 3)$ using $F$
$P(X \leqslant 1) + P(1 < X \leqslant 3) = P(X \leqslant 3)$
$\Rightarrow P(1 < X \leqslant 3) = F(3) - F(1)$

\[\therefore P(a < X \leqslant b) = F(b) - F(a)\]

Properties of CDF (필요충분조건, if and only if)

(1) increasing
(2) right continuous (우연속 계단 함수: 우극한을 가짐)
(3) $F(X) \to 0$ as $X \to -\infty$, $F(X) \to 1$ as $X \to \infty$

Independence of Random Variables

Defn. $X$, $Y$ are indep. r.v.s. if $P(X \leqslant x, Y \leqslant y) = P(X \leqslant x)P(Y \leqslant y)$ for all $x$, $y$.

Discrete case: $P(X = x, Y = y) = P(X = x)P(Y = y)$

Averages (Means, Expected Values)

[Example] Find avg. of 1, 1, 1, 1, 3, 3, 5
(1) add, divide: $\displaystyle \frac{1+1+1+1+3+3+5}{8}$
(2) use weighted avg.: $\displaystyle \frac{5}{8} \cdot 1 + \frac{2}{8} \cdot 3 + \frac{1}{8} \cdot 5$

$\frac{5}{8}$, $\frac{2}{8}$, $\frac{1}{8}$을 각각 가중치라고 부른다.

[Avg. of a discrete r.v. $X$]

\[E(X) = \sum_x xP(X=x)\]

• summed over $x$ with $P(X=x) > 0$

[Example 1] Bernoulli

[일반화] $X \sim Bern(p)$에 대해

\[E(X) = 1 \cdot P(X=1) + 0 \cdot P(X=0) = p\]

[예시] indicator r.v.에 대해

\[X = \begin{cases} 1, \text{if A occurs} \\ 0, \text{otherwise} \end{cases}, \text{then } E(X) = P(A)\]

교수님은 이를 fudamental bridge라고 부른다고 함 (종종 언급하심)

[Example 2] Binomial Distribution

$X \sim Bin(n, p)$에 대해서,

아래 Linearity 파트에 더 쉬운 방법도 있다.

[Example 3] Hypergeometric

5 card hand, $X = (\text{no. of} \ aces)$. Let $X_j$ be the indicator of j-th card being an ace. ($1 \leqslant j \leqslant 5$)

\[\begin{align*} E(X) &= E(X_1 + X_2 + X_3 + X_4 + X_5) && \text{(by indicator r.v.s)} \\ &= E(X_1) + \cdots + E(X_5) && \text{(by linearity)} \\ &= 5 \cdot E(X_1) && \text{(by symmetry)} \\ &= 5 \cdot P(\text{1st card ace})&& \text{(by fundamental bridge)} \\ &= \frac{5}{13} \end{align*}\]

even though $X_j$ s are dependet.
This gives expected value of any Hypergeometric.

Question
indicator r.v.s로 나타낼 때 ace는 총 4개 있어서 모든 위치에 j=1부터 j=5까지 모든 위치에 ace가 있는 경우가 포함되진 않는지..?

Answer
$X_j = 1$: j번째 카드가 ace
$X_j = 0$: j번째 카드가 ace가 아님
즉, $X = X_1 + X_2 + X_3 + X_4 + X_5$는 실제로 뽑힌 5장 중 ace의 개수를 세는 식이다.

• 예를 들어, 4장의 ace가 나왔을 때, 이는 1+1+1+0+1처럼 표현할 수 있다.
  결국, 모든 위치에 ace가 있는 경우 즉, $P(X_1=1, X_2=1, …, X_5=1) = 0$이 되기 때문에 그러한 경우가 포함되지 않는다.

[Example 4] Geometric Distribution

[Defn.]
$Geom(p)$: indep. $Bern(p)$ trials, count #. of failures before 1st success.
Let $X \sim Geom(p), q = 1-p$.

PMF: $P(X=k) = q^kp, \ k \in {0, 1, 2, \dots }$

• 유효한 PMF인지 확인
• $\displaystyle \sum^{\infty}_{k=0}pq^k = \frac{p}{1-q} = 1$

[Expectation]
(1) 수식 사용

(2) Story Proof
Let $C = E(X)$.
앞면이 나올 확률이 $p$인 동전을 반복해서 던지는 상황 가정

\[\begin{align*} C &= 0 \cdot p + (1 + C) \cdot q \\ &= q + Cq \\ &\Rightarrow C = \frac{q}{p} \end{align*}\]

Linearity

(1) $E(X+Y) = E(X) + E(Y)$ even if $X$, $Y$ are dependent.
(2) $E(CX) = CE(X)$ if $C$ is a constant.

[위 $Bin(n, p)$의 평균을 linearity로 증명]

$Bin(n, p)$는 $n$개의 확률이 $p$인 Bernoulli 시행을 했을 때의 분포이다.
즉, 각각의 $Bern(p)$는 기댓값 $p$를 갖고있고, 총 $n$ 개가 있으므로, 총 기댓값은 $np$이다.
(since $X = X_1 + X_2 + \cdots + X_n$, $X_j \sim Bern(p)$)