Lecture 07. Gambler's Ruin and Random Variables (Statistics 110, Harvard)
이 포스팅은 Harvard에서 진행된 Joe Blitzstein의 Statics 110 강좌를 기반으로 작성되었습니다.
Core Concept of Statistics
(1) Conditioning: The soul of statistics
(2) Random variables and distribution
Gambler’s Ruin
여기서 ruin은 bankrupt 즉, 파산을 뜻한다.
2 gamblers, A and B, sequence of rounds bet 1 dollar, $p=P(\text{A wins a certain round})$, $q=1-p$.
Find probability that A wins the entire game (so B is ruined).
assuming, A starts with $i$ dollars, B starts with $(N-i)$ dollars.
[(동치) Random Walk]
수직선 위의 임의의 위치 $i$ 로부터, $p$의 확률로 1 step씩 오른쪽으로 이동하는 상황을 가정할 수 있음.
- $p$: prob. of going right
- absorbing states at position 0, N
Let $p_i = P(\text{A wins game} \mid \text{A starts at } i \text{ dollar})$
[Strategy] condition on first step
\[p_i = pp_{i+1} + qp_{i-1}, \ 1 \leqslant i \leqslant N-1, \begin{cases} p_0 = 0 \\ p_N = 1 \end{cases} \ \text{(by LoTP)}\]- $pp_{i+1}$: A가 $p$ 의 확률로 이긴다면, $p_{i+1}$ 의 상황에서 동일한 과정을 반복
- $qp_{i-1}$: A가 $q$ 의 확률로 진다면, $p_{i-1}$ 의 상황에서 동일한 과정을 반복
difference equation (계차 방정식) 위 식과 같이 한 항이 다른 항에 의해 정의되는 방식을 말한다.
[Guessing을 통한 풀이]
$p_i = x^i$ 라고 가정한 뒤 문제를 해결해보자.
$x^i = px^{i+1} + qx^{i-1}$
$p^2 - x + q = 0$ ($x=1$ 대입하여 일반해 구하기)
$\displaystyle x = \frac{1 \pm \sqrt{1-4pq}}{2p}$ (근의 공식)
$1-4pq = 1-4p(1-p) = (2p-1)^2$ ($\sqrt{1-4pq}$ 에 $q=1-p$ 대입)
$p \neq q$ 를 가정하여 $x$ 에 대한 두 해가 다를 경우, 아래와 같은 선형 결합으로 표현
$p_i = x^i = A \cdot 1^i + B \cdot \frac{q}{p}^i$
$\displaystyle p_0 = 0 \Rightarrow B = -A, \ p_N = 1 \Rightarrow 1 = A(1-(\frac{q}{p})^N), \ \therefore A = \frac{1}{1-(\frac{q}{p})^N}$ (경계 조건을 사용해서 A, B를 구함)
$\displaystyle \therefore \frac{1-(\frac{q}{p})^i}{1-(\frac{q}{p})^N}, \text{ if } p \neq q$
$p=q$일 때는 극한을 적용
$\displaystyle x=\frac{q}{p}, \ \lim_{x \to 1} \frac{1-x^i}{1-x^N} = \lim_{x to 1} \frac{ix^i}{Nx^N} = \frac{i}{N}$ (by l’Hospital’s rule)
결과적으로, $p_i$ 는 다음과 같다.
\[\therefore\; p_i = \left\{ \begin{aligned} &\frac{1 - (q/p)^i}{1 - (q/p)^N}, && \text{if } p \neq q, \\ &\frac{i}{N}, && \text{if } p = q. \end{aligned} \right.\][불공정한 경우에 대해 살펴보기]
위 결론에서 $p \neq q$ 는 A 또는 B가 이길 확률이 동일하지 않은, 불공정한 상황을 말한다.
Let $i = N-i$ (같은 양의 돈), $p$ = 0.49
$N$ = 20 $\Rightarrow$ 0.40
$N$ = 100 $\Rightarrow$ 0.12
$N$ = 200 $\Rightarrow$ 0.02
즉, 약간만 불공평해도 처음 금액이 200일 때, B가 이길 확률이 98%나 된다.
[게임이 무한정 반복될 확률]
편의를 위해 p = q일 때만 빠르게 확인하고 넘어가자.
A와 B의 이름만 바꾸어 A가 파산할 확률은 $\displaystyle 1-\frac{i}{N} = \frac{N-i}{N}$ 이다.
두 확률을 더하면, $\displaystyle \frac{i}{N} + \frac{N-i}{N} = 1$, 즉, 둘 중 한 명이 파산할 확률의 합이 1이기 때문에 무한정 진행될 확률이 0이다.
Random Variables
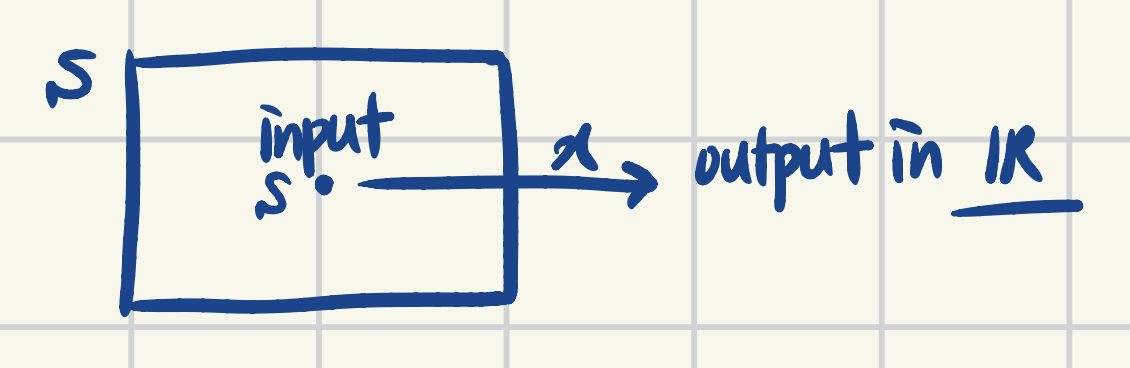
What is random variable? It’s a function from sample space $S$ to $\mathbb{R}$
[Example 1] Bernoulli Distribution
Defn. 확률 변수 $X$가 0(실패), 1(성공) 두 가지 값만 가질 수 있으며, $P(x=0) = p, P(x=0) = 1-p$ 일 때, $X$는 $Bernoulli(p)$ 분포를 따른다고 한다.
[Example 2] Binomial (n, p)
Defn. $n$번의 독립적인 $Bernoulli(p)$ 시행에서의 성공 횟수의 분포는 $Bin(n,p)$ 를 따른다고 한다.
이항확률변수의 확률질량함수(Probability Mass Function, PMF): $P(X=k) = p^k(1-p)^{n-k}, \ 0 \leqslant k \leqslant n, \ k \text{ is an integer}$
If $X \sim Bin(n,p)$, $Y \sim Bin(m, p)$, then $(X+Y) \sim B(n+m, p)$
proof consider $n$ trials, $m$ more trials
- $n$: 처음 $n$ 번의 시행 중 $X$의 성공 횟수
- $m$: 이후 $m$ 번의 시행 중 $Y$의 성공 횟수