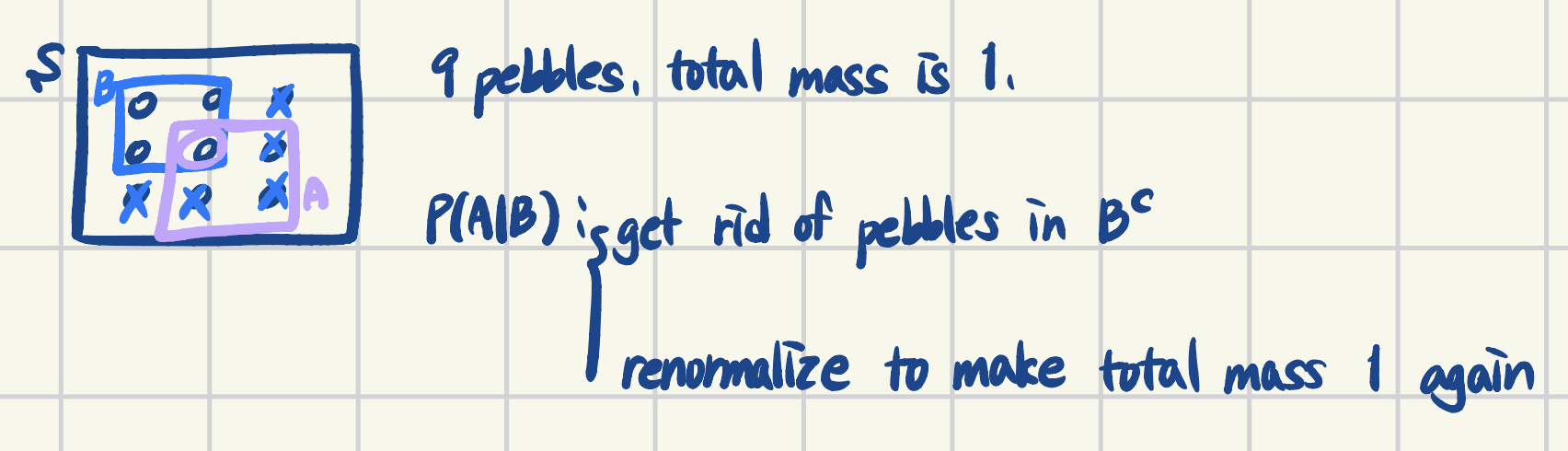Lecture 04. Conditional Probability (Statistics 110, Harvard)
이 포스팅은 Harvard에서 진행된 Joe Blitzstein의 Statics 110 강좌를 기반으로 작성되었습니다.
Independent (독립 사건)
Note: completely different from disjointness (배반 사건)
독립 사건: 사건 A가 사건 B에 전혀 영향을 미치지 않음
배반 사건: 사건 A와 사건 B가 동시에 일어날 확률이 0
Definition
Events A, B are independent if $P(A \cap B) = P(A)P(B)$.
Events A, B, C are independent if $P(A, B) = P(A)P(B)$, $P(B, C) = P(B)P(C)$, $P(C, A) = P(C)P(A)$, $P(A, B, C) = P(A)P(B)P(C)$.
Similarly for events $A_1, A_2, …, A_n$. "independent means multiply"
Newton-Pepys Problem (1693)
Have fair dice; which is most likely?
(A) at least one 6 with 6 dice
(B) at least two 6s with 12 dice
(C) at least three 6s with 18 dice
$P(A) = 1 - (\frac{5}{6})^6 \approx 0.665$
$P(B) = 1 - (\frac{5}{6})^{12} - \binom{12}{1}\frac{1}{12}(\frac{5}{6})^{11} \approx 0.619$
$P(C) = 1 - \sum^2_{k=0}\binom{18}{k}\frac{1}{6}^k(\frac{5}{6})^{18-k} \approx 0.597$
Conditional Probability
How should you update prob./beliefs/uncertainty based on new evidence?
Conditioning is the soul of statistics.
Definition
[Intuition 1] Pebble World
[Intuition 2] Frequentist World: repeat experiments many times
Theorems of Conditional Probability
[Theorem 1]
\[P(A \cap B) = P(B)P(A|B) = P(A)P(B|A)\][Theorem 2]
\[P(A_1, ..., A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1, A_2) \cdots P(A_n|A_1, A_2, ..., A_n)\][Theorem 3]
\[P(A|B) = \frac{P(B|A)P(A)}{P(B)} \ \text{Bayes' Rule} \ (\because \text{Theorem 1})\]