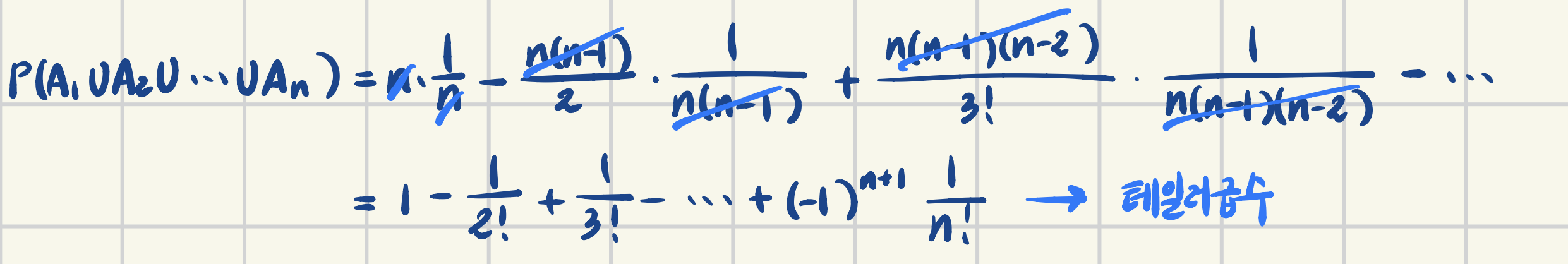Lecture 03. Birthday Problems, Properties of Probabilities (Statistics 110, Harvard)
이 포스팅은 Harvard에서 진행된 Joe Blitzstein의 Statics 110 강좌를 기반으로 작성되었습니다.
Birthday Problem
$k$명의 사람들 중에서, 최소 2명의 생일이 같을 확률을 구하여라.
assume, no Feb. 29th, and other 365 days are equally likely; assume independence of birth.
if $k > 365$, prob. is 1 (pigeonhole principle).
else $k \leqslant 365$, (아직 근사 적용 X, 수식만 보기)
\[P(\text{no match}) = \frac{365 \cdot 364 \cdot 363 \cdots (365-k+1)}{365^k} \\ P(\text{match}) \approx \begin{cases} 50.7\% & \text{if } k = 23 \\ 99\% & \text{if } k = 50 \\ 99.999\% & \text{if } k = 100 \end{cases}\]50%나 된다고!? 하는 경우를 위해…
$\binom{k}{2} = \frac{k(k-1)}{2}$를 사용해서, $\binom{23}{2} = \frac{23 \cdot 22}{2} = 253$
23명 중 생일이 같은 2명을 선택하는 경우의 수가 253이기 때문에, 365의 50%와 유사하다고 볼 수 있다.
(remind) Axioms of Probability
(1) $P(\varnothing) = 0, P(S) = 1$
(2) $P(\bigcup^{\infin}{n=1} A_n) = \sum^\infin{n=1}P(A_n)$ if $A_1, A_2, …$ are disjoint events.
Properties
(1) $P(A^C) = 1 - P(A)$
pf. $1 = P(S) = P(A \cup A^C) = P(A) + P(A^C)$, since $A \cap A^C$
(2) If $A \subseteq B$, then $P(A) \leqslant P(B)$
pf. $B = A \cup (B \cap A^C)$, $A$ and $B \cap A^C$ are disjoint events
$\therefore P(B) = P(A) + P(B \cap A^C) \geqslant P(A)$
(3) $P(A \cup B) = P(A) + P(B) - P(A \cap B)$
pf. $P(A \cup B) = P(A \cup (B \cap A^C)) = P(A) + P(B \cap A^C)$ (disjointification)
$P(A \cap B) + P(B \cap A^C) = P(B)$ is true since $A \cap B$, $A^C \cap B$ are disjoint, $P(B \cap A^C) = P(B) - P(A \cap B)$.
$\therefore P(A) + P(B \cap A^C) = P(A) + P(B) - P(A \cap B)$
Inclusion-Exclusion (포함 배제의 원리)
\[P(A_1 \cup A_2 \cup \cdots \cup A_n) = \sum^n_{i=1}P(A_i) - \sum_{i<j}P(A_i \cap P_j) + \sum_{i<j<k}P(A_i \cap A_j \cap A_k) - \cdots + (-1)^{n+1}P(A_1 \cap A_2 \cap \cdots \cap A_n)\]deMontmort’s Problem (1713), matching problem (using inclusion-exclusion)
$n$개의 카드를 섞었을 때, 최소 한 장의 카드 $k$가 $k$번째 자리에 위치할 확률
Let $A_j$ be the event “$j$-th card matches”
$P(A_j) = \frac{1}{n}$ since all positions are equally likely for card labeled $j$.
$P(A_1 \cap A_2) = \frac{(n-2)!}{n!} = \frac{1}{n(n-1)}$ since 1, 2번 카드만 제자리에 있고, 나머지는 랜덤하게 나열
…
$P(A_1 \cap A_2 \cap \cdots \cap A_k) = \frac{(n-k)!}{n!}$
$\therefore \frac{1}{e}$로 수렴