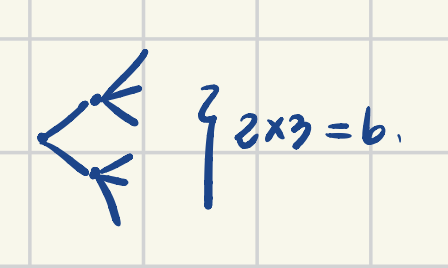Lecture 01. Probability and Counting (Statistics 110, Harvard)

이 포스팅은 Harvard에서 진행된 Joe Blitzstein의 Statics 110 강좌를 기반으로 작성되었습니다.

• 강의 및 자료 링크

용어 정리

A sample space is the set of all possible outcomes of an experiment An event is a subset of the sample space

Naive Definition of Probability

\[P(A) = \frac{\text{# of favorable outcomes}}{\text{# of possible outcomes}}\]

Assumes that all outcomes are equally likely and has finite sample space.

Counting

Multiplication Rule (곱의 법칙)
if have experiment with $n_1$ possible outcomes, and for each outcome of first experiment, there are $n_2$ possible outcomes for 2nd experiment, …, for each outcome of $n_r$ outcomes for $r$-th experiment, then $n_1n_2…n_r$ overall possible outcomes.

[Ex. 1] Ice Cream
if have 2 cones and 3 flavors,
total possible outcomes are $2 \times 3 = 6$.

[Ex. 2] Ful House (5장 중 같은 수 각각 3장, 2장)

[참고] Binomial Coefficient (이항 정리)
$\binom{n}{k} = \frac{n!}{(n-k)!k!}\text{ only if }(k > n)$

전체 공간: 52장의 카드 중에서 5장 선택
사건이 일어날 경우의 수: {13개 숫자 중 하나 선택 x 네 개 문양 중 택 3} x {나머지 12개 숫자 중 하나 선택 x 네 개 문양 중 택 2}

\[\frac{13 \cdot \binom{4}{3} \times 12 \cdot \binom{4}{2}}{\binom{52}{5}}\]

Sampling Table: choose $k$ objects out of $n$

	order matter	order doesn’t
replace	$n^k$	$\binom{n+k-1}{k}$
don’t replace	$n(n-1)…(n-k+1)$	$\binom{n}{k}$