Post

Lecture 4. Model-Free Prediction

Posted
By oceann
14 min read

이 포스팅은 David Silver의 RL 강좌를 기반으로 작성되었습니다.

Introduction

지난 강의에서,

  • Planning by DP
  • MDP를 아는 상황을 가정함
    • 즉, environment를 대변하는 model이 있음을 가정
    • model은 $\mathcal{P}$ (transition prob.)를 알기 때문에 next state와 reward의 정보를 제공

이번 강의에서,

  • Model-free Prediction을 공부
  • 즉, unknown MDP의 상황에서 value fn.을 구하는 방법
  • offline method: 하나의 episode가 완전히 terminate 되었을 때 업데이트하는 방식, Monte-Carlo
  • online method: 하나의 episode 내의 step마다 업데이트하는 방식, Temporal-Difference

다음 강의에서,

  • Model-free control을 공부
  • 즉, value fn. 예측을 기반으로 최적의 value fn.을 구하는 방법

Monte-Carlo Learning (Offline Method)

[ Monte-Carlo Reinforcement Learning ]

  • MC는 episode의 경험으로부터 직접 파악함
  • MDP의 transition과 reward를 몰라도 적용 가능
    • environment 전부를 아는 것이 아니라, 일부 state와 action을 샘플링하여 정보를 얻는 것
    • Ex. 원의 넓이를 구하는 방법이 무지하게 복잡하다고 했을 때, 원에 해당하는 공간에 무수히 많은 점을 찍어 원의 넓이를 추정하는 것 → 점을 찍는 경험(experience)을 통해 원의 넓이(value)를 구함
  • 하나의 완전한 episode로부터 학습
    • offline 방식이라고 부름
    • no bootstrapping
  • $\text{value} = \text{mean return}$ 이라는 가장 단순한 아이디어를 적용
  • 하나의 episode가 완전히 종료되어야 하기 때문에 terminate state가 반드시 정의되어야 함

[ Monte-Carlo Policy Evaluation ]
목표: policy $\pi$ 가 주어졌을 때, 여러 episode로부터 $v_\pi$ 를 학습하는 것

\[S_1, A_1, R_2, ..., S_k \sim \pi\]
  • 기존의 value fn.: 현재 state로부터 return에 대한 기댓값 ($\because$ 모든 전이 확률과 reward를 알고 있음)
  • MC의 value fn.: 샘플링된 경험들 중 return에 대한 평균값
\[v_\pi(s) = \mathbb{E}_\pi[G_t | S_t=s]\]
  • Monte-Carlo policy evaluation은 기댓값 대신에, 경험적으로 episode들을 탐색 후 얻는 reward들의 평균값을 의미

first-visit MC vs. every-visit MC

state $s$ 를 평가하기 위해 특정 state $s$를 방문한 순서에 따라 reward의 평균을 다르게 구함
기본적으로, 아래의 알고리즘을 따름

  • when visit $s$,
  • increment counter: $N(s) \gets N(s)+1 $
  • increment total return: $S(s) \gets S(s)+G_t $
  • value is estimated by mean return $V(s) = S(s) / N(s) $
  • by law of large numbers(큰 수의 법칙), $V(s) \to v_\pi(s)$ as $ N(s) \to \infty $
1
2

episode: S1 → S2 → S1 → S3 → terminal
rewards: 1  → 2  → 3  → 4  → 0

[ First-Visit Monte-Carlo Policy Evaluation ]

  • 각 episode 내에서 어떤 상태 $s$ 가 처음 등장했을 때만 이후의 return을 계산해서 해당 state의 value fn.을 업데이트

[ Every-Visit Monte-Carlo Policy Evaluation ]

  • 각 episode 내에서 어떤 상태 $s$ 가 등장할 때마다 이후의 return을 계산해서 해당 state의 value fn.을 업데이트

Incremental Monte-Carlo

모든 episode들이 끝난 뒤에 sum을 평균내지 않고, episode가 끝날 때마다 online방식처럼 update 할 수 있음

[ Incremental Monte-Carlo Updates ]

Incremental Mean (산술 평균) LaTeX이 귀찮아 손필기로 대체...
  • Incremental Mean에 의해 모든 episode들을 수집한 뒤에 업데이트하지 않고, 하나의 episode가 종료되었을 때 업데이트 할 수 있음
  • 각 state $S_t$ 의 return이 $G_t$ 일 때
    • $N(S_t) \gets N(S_t)+1$
    • $V(S_t) \gets V(S_t) + \frac{1}{N(S_t)} (G_t - V(S_t))$
    • $\frac{1}{N(S_t)}$ 로 나누는 단순 평균이기 때문에 시간 정보를 반영하기 어려움 (stationary에 적합)
  • 시간에 따라 변하는 환경(non-stationary)에 경우, 과거의 정보를 점점 잊는 것이 중요함
    • running mean을 적용
    • $V(S_t) \gets V(S_t) + \alpha (G_t - V(S_t))$
    • $\alpha$ 는 learning rate로써, 1보다 작을 경우 시간에 따라 서서히 과거 정보를 잊게 하는 역할
environment $\alpha$ 의미
stationary $\frac{1}{N(S_t)}$ 모든 episode에 대해 동일한 가중치로 평균
non-stationary 고정된 작은 상수 (e.g. 0.1) 최근 episode의 중요도를 더 높임(과거 서서히 잊기)

Temporal-Difference Learning (Online Method)

  • episode의 경험으로부터 직접 학습
  • MC와 같이 model-free 방식
  • episode가 종료되지 않아도 즉, 불완전한 episode로부터 학습이 가능
    • bootstrap: episode가 끝날 때까지 기다리지 않고, 다른 estimated value를 활용해서 현재 state를 eval
    • 즉, guess로부터 guess를 업데이트

[ Monte-Carlo & Temporal-Difference ]

  • 잠깐 MC recap
    • MC가 offline method인 이유: $G_t$ 는 최종 return이기 때문에 현재 state로부터 terminal state까지의 값을 모두 알아야 함
\[V(S_t) \gets V(S_t) + \alpha(G_t - V(S_t))\]
  • 반면에 Temporal-Difference learning에서는… (TD(0) 기준으로)
    • episode가 종료될 때까지 기다리는 게 아니라, 현재 state에서 다음 state의 결과만 확인한 뒤 업데이트를 수행
    • $G_t$ 대신에 Bellman Expected Equation을 사용
\[V(S_t) \gets V(S_t) + \alpha(R_{t+1}+\gamma V(S_{t+1}) - V(S_t))\]
  • $R_{t+1} + \gamma V(S_{t+1})$: TD target
  • $\delta_t = R_{t+1}+\gamma V(S_{t+1}) - V(S_t)$: TD error

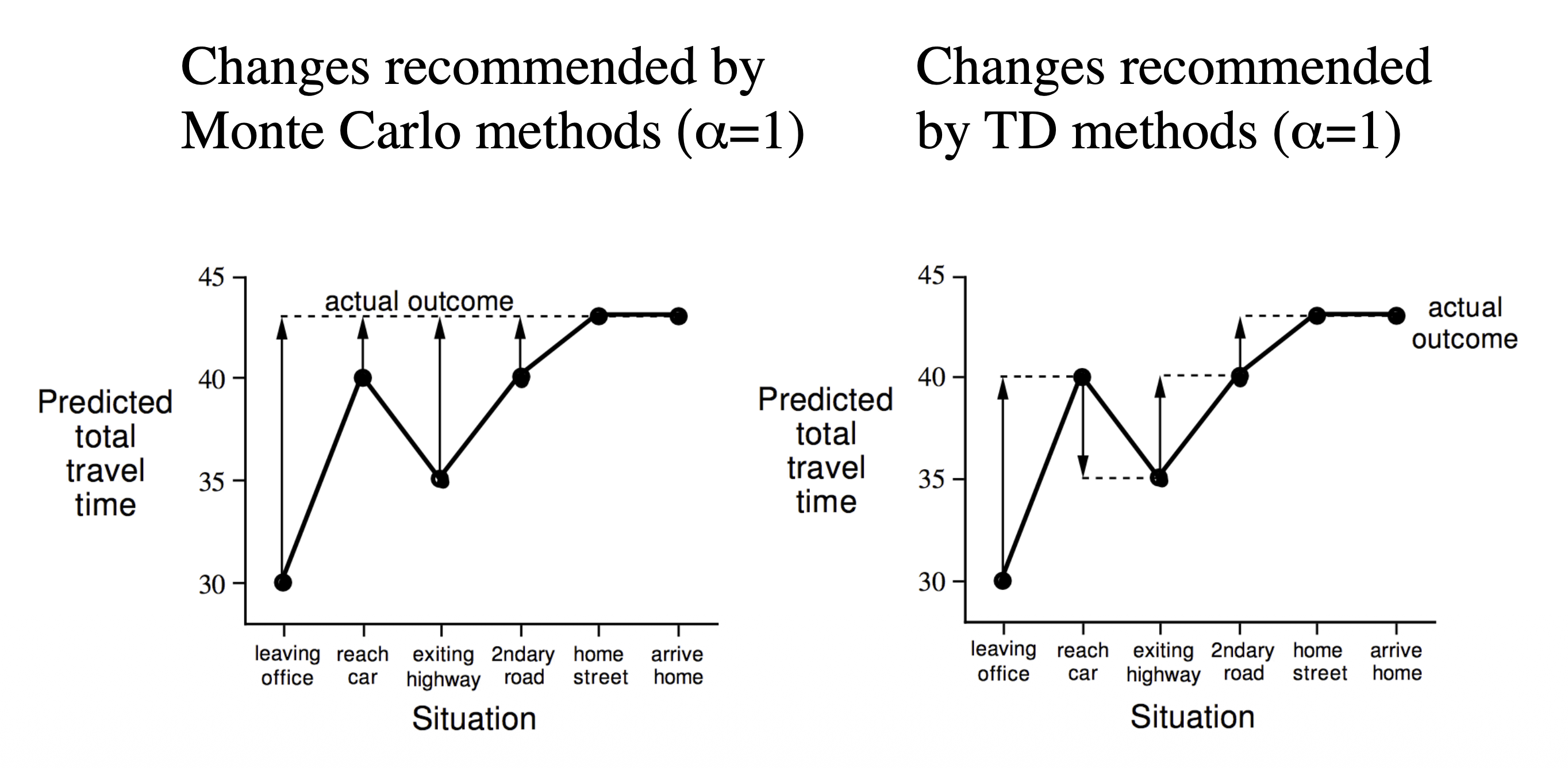
[ MC vs. TD: Driving Home Example ]

State Elapsed Time (minutes) Predicted Time to Go Predicted Total Time
leaving office 0 30 30
reach car, raining 5 35 40
exit highway 20 15 35
behind truck 30 10 40
home street 43 0 43
  • 왼쪽: Monte-Carlo
    • 하나의 episode가 종료되었을 때, 각 state를 최종값으로 업데이트
    • episode가 종료되었을 때가 되어서야 비로소 모든 state를 동시에 업데이트 할 수 있음 (state별 업데이트가 느림)
  • 오른쪽: Temporal-Difference
    • 현재 state에서 다음 state의 Predicted Total Time을 보고, 해당 값으로 업데이트
    • 오직 다음 step만 확인하고 현재 state를 업데이트 할 수 있음 (state별 업데이트가 빠름)
      • 다음 state에서의 예측값으로 업데이트 하기 때문에 expectation으로부터 expectation을 업데이트 (bootstrapping)

[ MC vs. TD: advantages & disadvantages ]

  TD MC
When to Update - 한 step 이후에 value를 알 수 있음
- 불완전한 sequence 내에서도 value를 알 수 있음
- non-terminating 환경에도 적용 가능		 - episode가 종료되고 return을 알아야 함
- 완전한 sequence 내에서만 value를 알 수 있음
- episodic 환경에서만 적용 가능
Bias&Variance low variance, some bias
- 주로 MC보다 효율적임
- TD(0)는 $v_\pi(s)$ 로 수렴이 보장됨
- 초기값에 영향을 크게 받음		 high vairance, zero bias
- 항상 최적으로 수렴을 보장
- 초기값의 영향이 작음
- 단순하고 적용이 쉬움
Makrov Markov property를 탐색
($\because$ next state를 확인해야 함)		 non-Markov에 더 적합
($\because$ 모든 가능한 state들을 직접 탐색)
Bootstrapping O X
Sampling O O
  • bias: 실제 기댓값과 현재의 추정값이 다른지 (예측이 포함되었는지, 경험적인 결과인지)
  • variance: 데이터 자체의 값의 변동이 큰지 (실세계의 값일 수록 noisy한 경향이 있음)
  • bootstrapping: 업데이트가 예측을 동반하는지 (DP는 O)
  • sampling: 모든 경우를 대표하는 기댓값을 활용하는지 (DP는 X)

Batch MC & TD

  • $k$ step을 사전에 정의해두고, 해당 episode 또는 step만큼 샘플링한 뒤, MC/TD error를 계산해서 업데이트를 수행하는 방법

TD($\lambda$)

n-step TD

  • 앞서 설명한 TD(0)는 one-step lookahead로, 빠르지만 bias 존재
  • MC는 bias가 없지만 terminate state까지 기다려야 함
  • 둘을 조합하여 n-step lookahead를 수행하는 TD를 구현한다면?

[ n-Step Return ]

  • n-step return은 다음과 같음
    • n=1: $G_t^{(1)} = R_{t+1} + \gamma V(S_{t+1})$
    • n=2: $G_t^{(2)} = R_{t+1} + \gamma V(S_{t+2}) + \gamma^2V(S_{t+2})$
    • …
    • n=$\infty$ (MC): $G_t^{\infty} = R_{t+1} + \gamma V(S_{t+2}) + … + \gamma^{T-1}R_T$
  • n-step return: $G_t^{(n)} = R_{t+1} + \gamma V(S_{t+2}) + … + \gamma^nV(S_{t+n})$
  • n-step TD learning: $V(S_t) \gets V(S_t) + \alpha (G_t^{(n)} - V(S_t))$

[ Averaging n-Step Returns ]

  • n-step return에 대해서 step이 달라질 때마다 정보량이 다름
  • $\lambda$-return: 모든 n-step들의 return인 $G_t^{(n)}$ 을 결합
\[G_t^{\lambda} = (1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}G_t^{(n)}\]
  • $1-\lambda$: normalizing factor로, 가중치항만 볼 때 총합이 1이 되도록 보정하는 역할
  • $\lambda$: weight decay parameter로, n-step에 따라 그 영향력을 조정

Forward-View TD($\lambda$)

\[V(S_t) \gets V(S_t) + \alpha (G_t^\lambda - V(S_t))\]
  • 현재 state $S_t$ 에서 다음 state, 또 그 다음 state를 순차적으로 살펴보는 방식 → MC처럼 완전한 episode일 때 적용 가능
  • 1-step부터 terminate state까지 누적해야 하기 때문에 이론적으로만 가능함

Backward-View TD($lambda$)

  • backward-view TD는 forward-view TD와 동치이지만, 실현 가능한 방법
  • online으로, 매 step마다, 불완전한 episode에 적용 가능한 방법

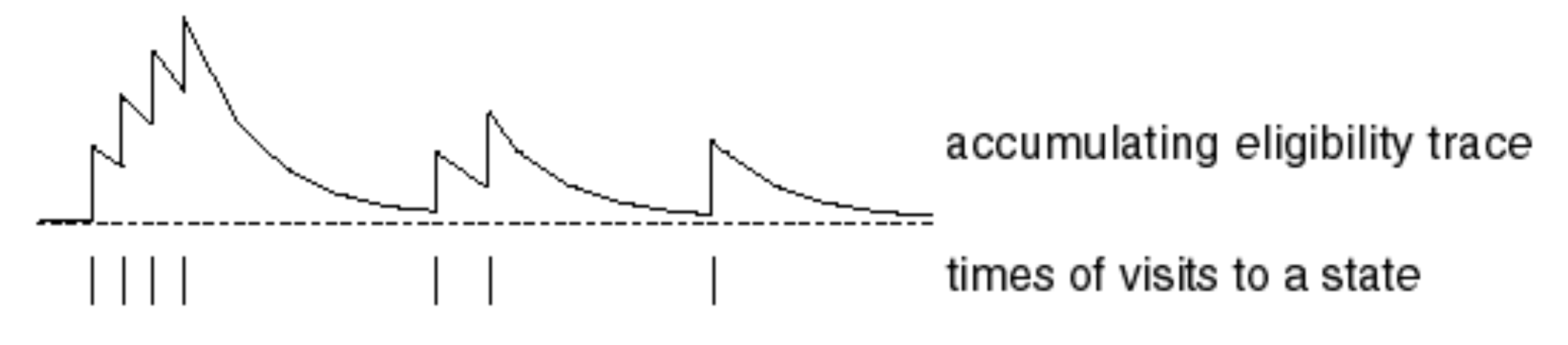
[ Eligibility Traces ]
frequency heuristic과 recency heauristic을 결합하여 방문한 state의 상태를 기록하는 방법

  • frequency heuristic 자주 방문한 state의 중요도를 높임
  • recency heuristic 최근에 방문한 state의 중요도를 높임
\[E_0(s) = 0 \\ E_t(s) = \gamma \lambda E_{t-1}(s) + 1(S_t=s)\]
  • $\gamma \lambda$: timestep이 멀어질 수록 영향력이 감소 (recency hearistic)
    • $\gamma$: discount factor, 미래 보상의 중요도는 감소되어야 함 (TD error를 구할 때도 사용됨)
      • discount factor를 과거의 Eligibility Trace에 곱하는 이유
        • 현재 timestep에서 특정 state의 eligibility trace 값이 바뀌면, 해당 값을 과거 timestep의 해당 state에 반영해야 함
        • 이때, 현재 timestep에서 멀수록 그 영향력을 작게 전달해야 함
    • $\lambda$: weight decay parameter, 시간이 지나면 과거의 정보는 점점 희미해져야 함
  • $1(S_t=s)$: timestep $t$ 에 방문한 state가 현재 state $s$ 와 동일하면 +1 (frequency hearistic)

[ Backward-View TD($\lambda$) ]

\[\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \\ V(S) \gets V(s) + \alpha \delta_t E_t(s)\]
  • 앞서 정의한 eligibility traces($E_t(s)$)를 TD($\lambda$)에 반영
  • 현재 timestep $t$ 에서 발생한 TD error($\delta_t$)가 eligiblity traces로 인해 과거 발생한 value fn.에도 영향을 줌 (아래 예제로 확인)

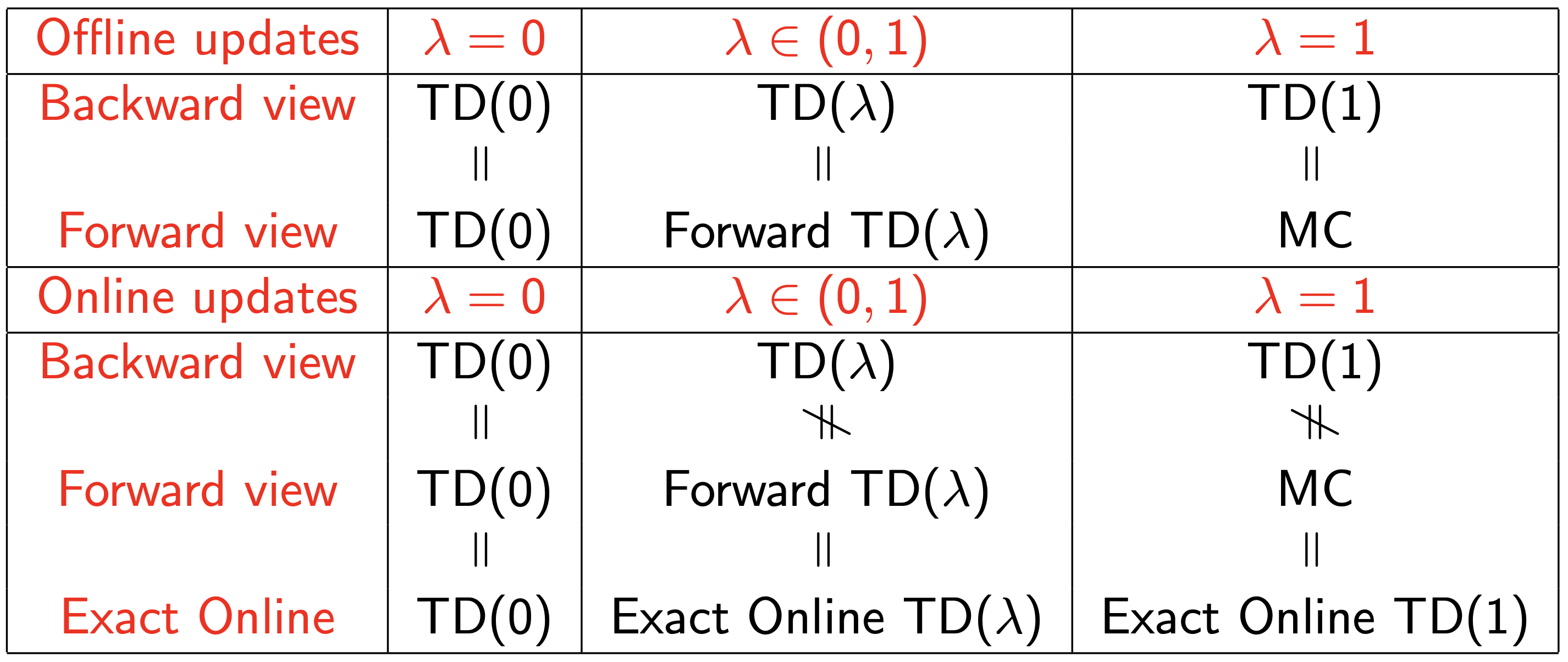
Forward and Backward Equivalence

(교안에는 근사를 통해 증명하는 과정이 있지만, 강의에서도 스킵했으니 나도 패스…0_<)

Offline updates…

  • episode 내에 업데이트를 누적해둠
  • episode가 종료되었을 때 배치로 업데이트

Online updates…

  • TD($\lambda$)는 각 episode 내의 매 step마다 업데이트
  • forward & backward-view TD($\lambda$)는 살짝 다를 수 있음
  • eligibility trace를 활용한 정확한 online TD($\lambda$)는 완벽하게 동치

[ Summary of Forward and Backward TD($\lambda$) ]

RL, David Silver
RL
This post is licensed under CC BY 4.0 by the author.