Lecture 3. Planning by Dynamic Programming
이 포스팅은 David Silver의 RL 강좌를 기반으로 작성되었습니다.
Introduction
[ Dynamic Programming이란? ]
복잡한 문제를 단순한 subproblem으로 쪼개어 해결하는 방법
[ Requirements for DP ]
- 두 가지 요소를 충족해야 함
- 최적의 해결방법은 subproblem들로 쪼개질 수 있어야 함
- 쪼개진 subproblem들에 겹치는 부분이 있어 caching이 가능해야 함
- MDP는 두 가지 요소를 모두 충족
- Bellman Equation을 통해 반복적으로 문제를 쪼갤 수 있음
- value fn.은 저장되고, 재사용 가능
[ Planning by DP ]
- DP는 MDP의 모든 상황을 알고 있음을 가정
- model-free: env가 어떤지 모르며, 완전한 정보를 얻을 수 없음 → DP 적용 X (모든 state에 대해 backup하는 게 아닌, sample backups는 model-free 환경이 적용될 수 있음)
- model-based: env에 대한 model이 있어 모든 상황을 아는 경우 → DP 적용 O
for Prediction
- Input: MDP $<\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma>$ & policy $\pi$ or MRP $<\mathcal{S}, \mathcal{P}^\pi, \mathcal{R}^\pi, \gamma>$
- Output: value fn. $v_\pi$ (즉, 목표가 value fn.을 예측하는 것)
for Control
- Input: MDP $<\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma>$
- Output: 최적의 value fn. $v_$ 와 최적의 policy $\pi_$
DP는 RL에서 뿐만 아니라 다양한 문제 해결에 사용되지만, 본 강의와는 관련 없기 때문에 생략!
Policy Evaluation
Iterative Policy Evaluation
Problem
policy $\pi$ 가 주어졌을 때, 해당 policyd의 reward를 계산하는 것
Solution
반복적으로 Bellman Expectation을 적용 ($v_1 \to v_2 \to … \to v_\pi$)
이때, synchronous backups(caching)를 활용 (asynchronous backups는 아직 고려하지 않음)
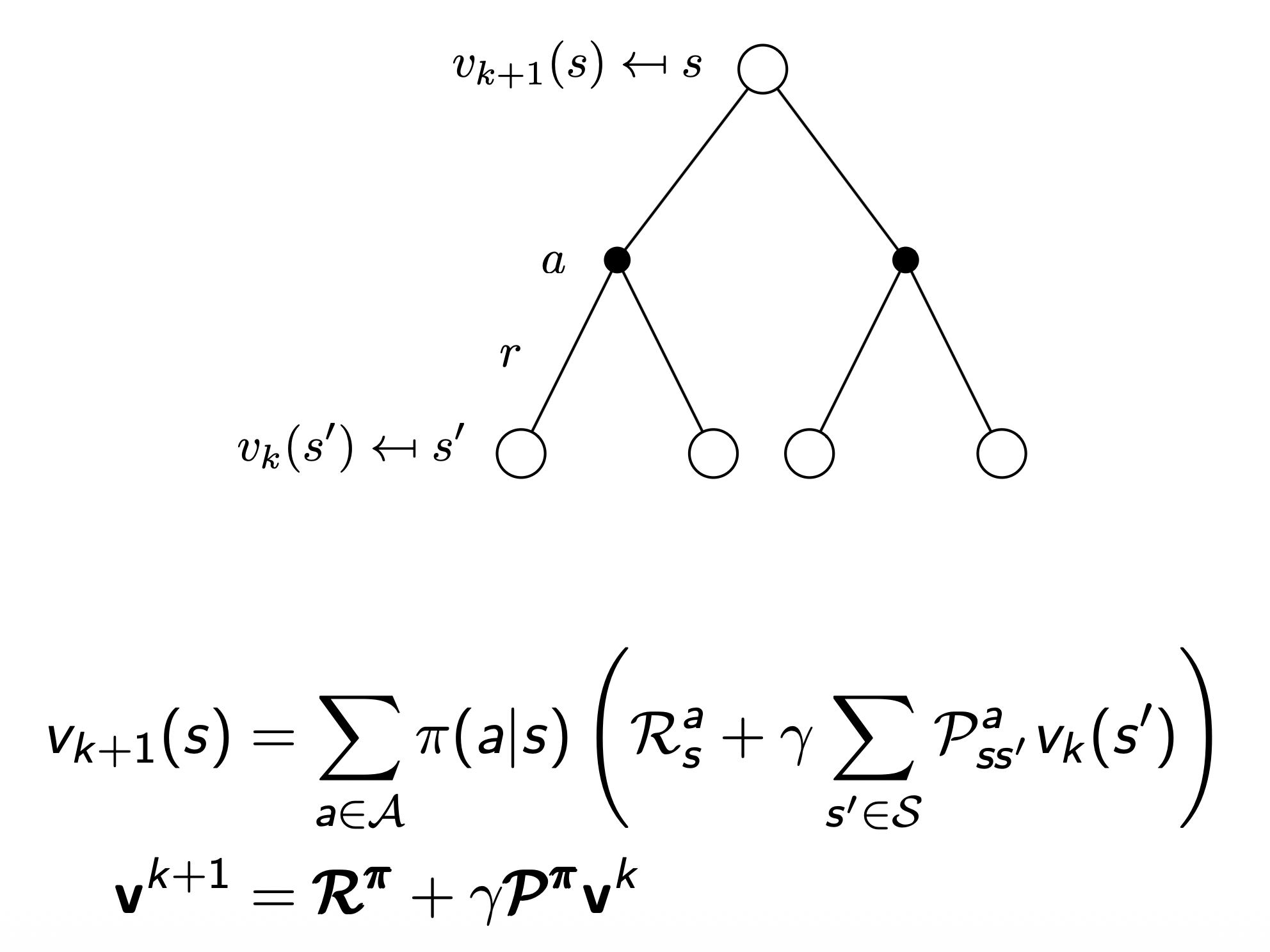
- 각 iteration step $k+1$ 일 때,
- 모든 state $s \in S$ 에 대해서,
- $v_k(s’)$ 를 활용해서 $v_{k+1}(s)$ 를 업데이트 (이때, $s’$ 은 $s$ 로부터 도달 가능한 다음 state)
$v_\pi$ 로 반드시 수렴하는 것을 본 강의에서 증명
state $s$ 에서 action $a$ 수행 → 다음 모든 state $s’$ 들의 값을 사용해서 현재 state의 value fn. $v_{k+1}(s)$ 를 정확히 예측
- $\pi(a \mid s)$: 현재 state $s$ 에서 수행할 수 있는 action $a$ 에 대한 policy
- $\mathcal{R}_s^a$: 현재 state $s$ 에서 action $a$ 를 수행할 때 받는 immediate reward
- $\gamma$: discount factor
- $\mathcal{P}^a_{ss’}$: 현재 state $s$ 에서 다음 state $s’$ 로의 전이 확률(action $a$ 를 수행했을 때)
- $v_k(s’)$: 다음 state $s’$ 에서의 value fn.
Example: Small Gridworld
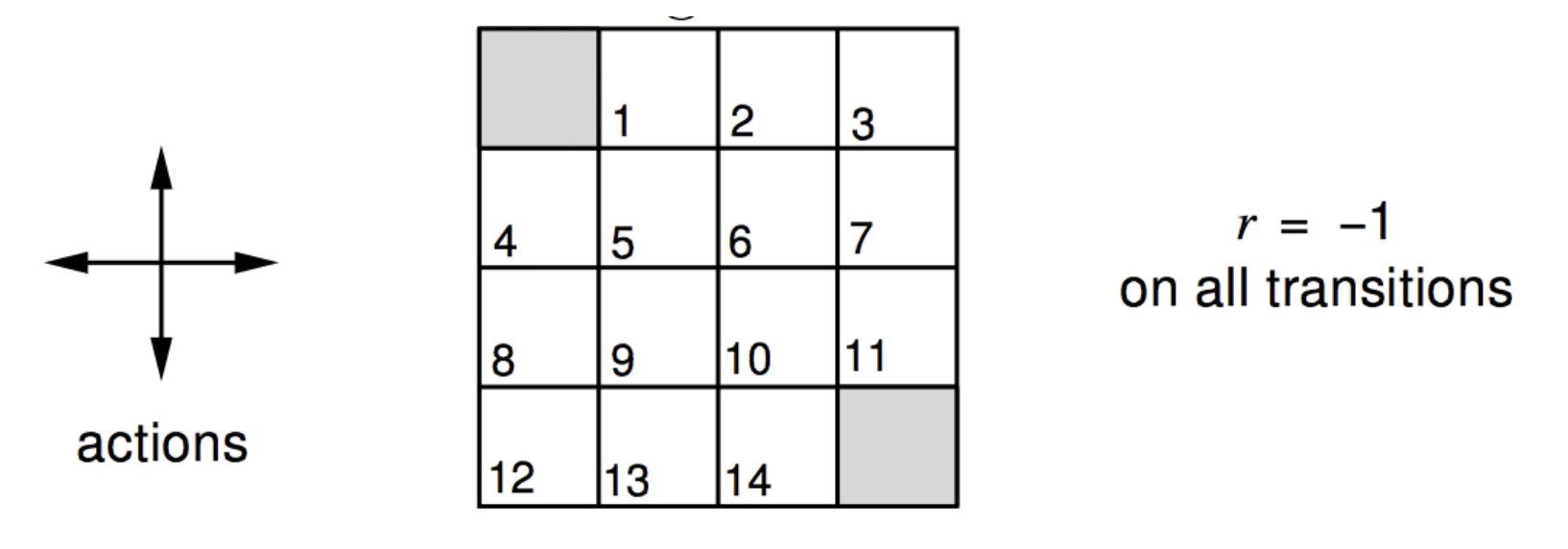
[ 조건 ]
- undiscounted episodic MDP ($\gamma = 1$)
- 1, …, 14는 nonterminal state들
- 회색 박스들이 terminal state들
- 그리드 밖을 나가는 action을 수행할 경우, 원래의 위치로 되돌아오게 됨
- terminal state에 도달하기 전까지 모든 transition의 reward는 -1
- agent는 아래의 랜덤 policy를 따름 (랜덤 policy에서부터 시작하더라도, 결국 최적의 policy에 도달)
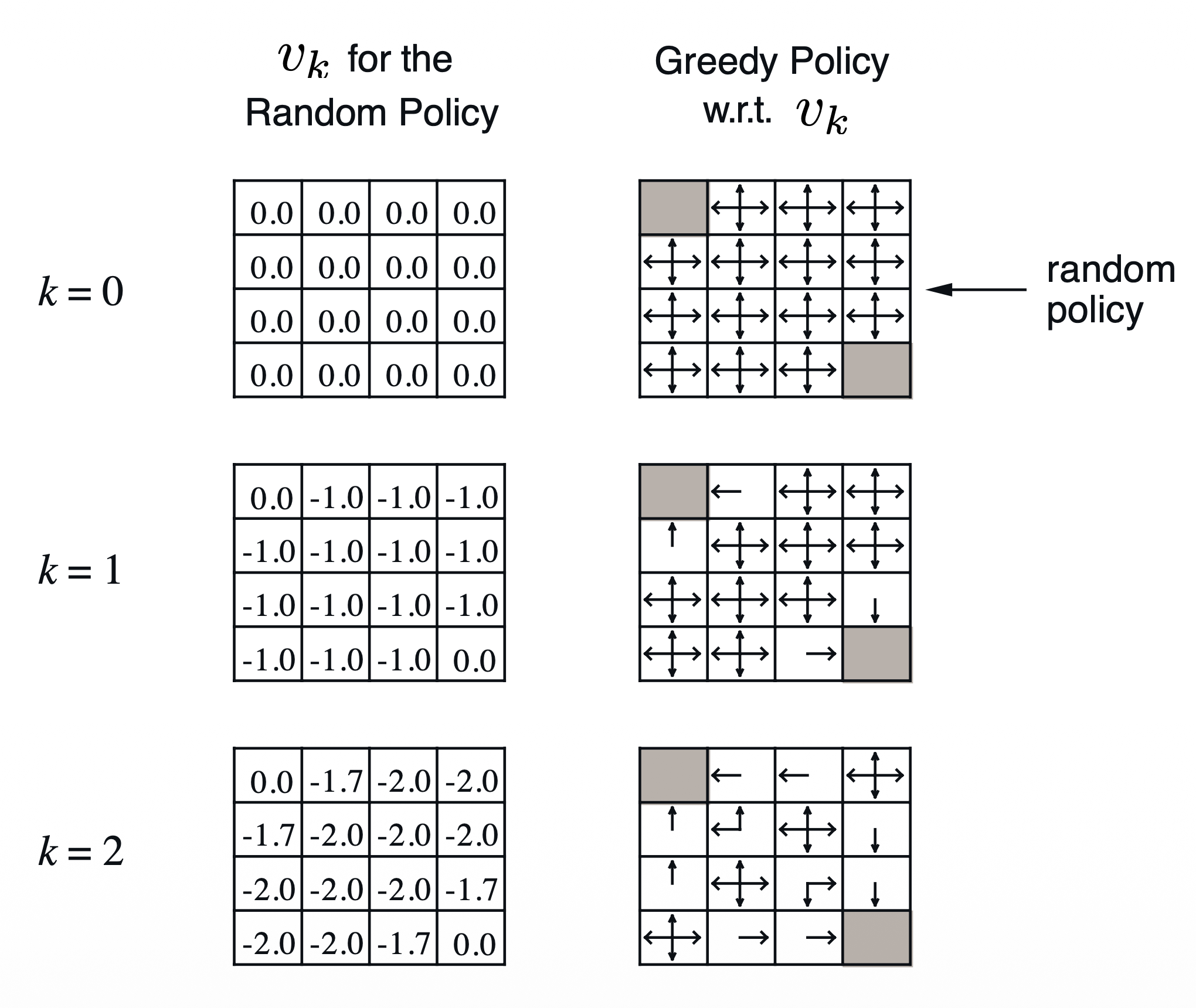
계산 예시: north, east, south, west 순서대로 계산
k=2, box 1 0.25(-1.0-1.0) + 0.25(-1.0-1.0) + 0.25(-1.0-1.0) + 0.25(-1.0+0.0) = -1.75 $\approx$ -1.7
k=2, box 5 0.25(-1.0-1.0) + 0.25(-1.0-1.0) + 0.25(-1.0-1.0) + 0.25(-1.0-1.0) = -2.0
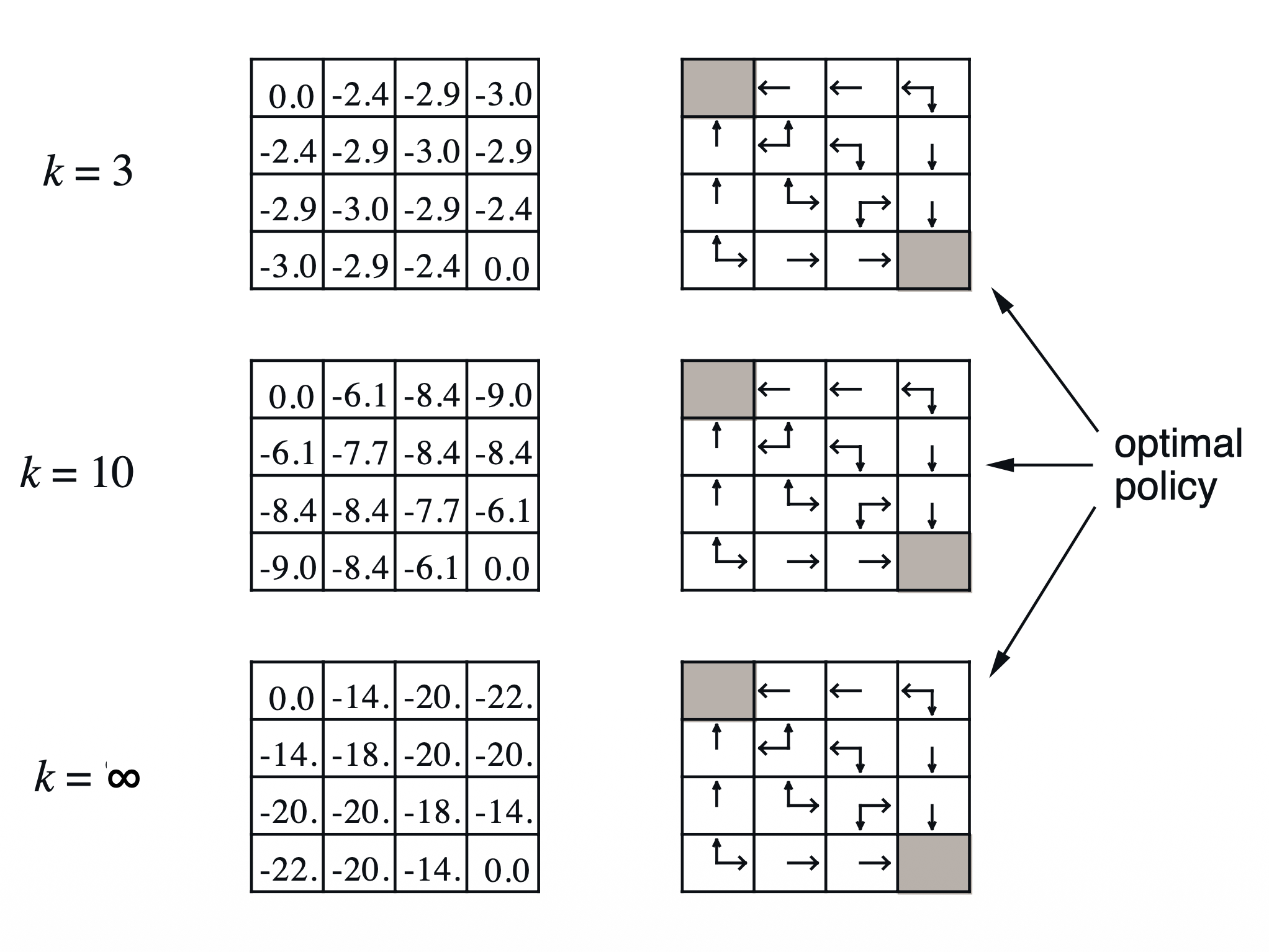
k=3, box 1 0.25(-1.0-1.7) + 0.25(-1.0-2.0) + 0.25(-1.0-2.0) + 0.25(-1.0+0.0) = -2.425 $\approx$ -2.4
(그림을 보면, value fn.이 전부 업데이트가 되지 않았음에도 policy는 최적을 찾은 상태인데, 이는 뒤에 더 자세히 설명될 것~)
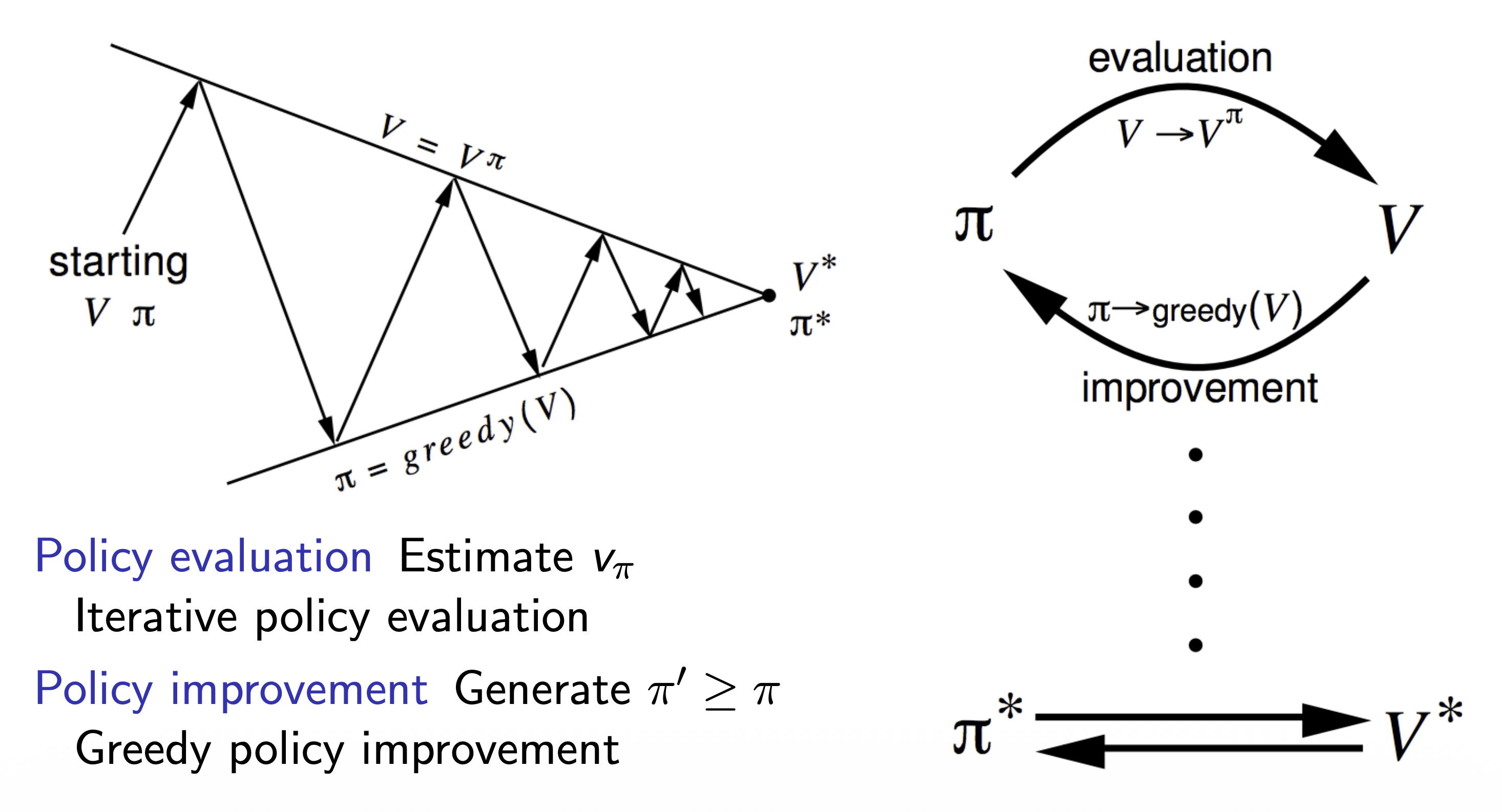
Policy Iteration
How to Improve Policy
policy $\pi$ 가 주어졌을 때, 해당 policy의 value fn. $v_\pi$ 를 계산
\[v_\pi(s) = \mathbb{E}[R_{t+1} + \gamma R_{t+2} + ... | S_t=s ]\]계산해서 얻은 $v_\pi$ 에 따라서 매 스텝마다 greedy하게 policy를 업데이트
\[\pi ' = \text{greedy}(v_\pi)\]Small Gridworld에서 봤던 예제에서도 $\pi ‘ = \pi^$ 로 수렴함을 확인
실제 문제들에 접목했을 때는 더 많은 iteration을 거쳐야 하지만, 어떠한 경우에도 policy iteration은 반드시 최적의 policy $\pi^$ 로 수렴함
policy evaluation과 policy improvement를 반복적으로 수행
- policy evaluation: $v_\pi$ 를 계산
- policy improvement: 계산한 $v_\pi$ 를 통해 greedy하게 policy를 업데이트
Policy Improvement
[ 반드시 최적의 value fn. & policy로 수렴하는 것을 증명 ]
- deterministic policy 가정: $a = \pi(s)$
- 매 스텝마다 greedy하게 policy를 업데이트: $\pi’(s) = \operatorname*{argmax}\limits_{a \in \mathcal{A}} q_\pi(s,a)$
- $q_\pi(s, a)$: 특정 action $a$를 수행했을 때 얻는 value fn.
- 즉, 수행 가능한 여러 action들 중에 argmax를 통해 최적의 action을 다음 policy $\pi’$ 으로 선택하겠다는 것
- policy를 업데이트함에 따라 value 또한 업데이트: $q_\pi(s, \pi’(s)) = \operatorname*{max}\limits_{a \in \mathcal{A}} q_\pi(s, a) \ge q_\pi(s, \pi(s)) = v_\pi(s)$
- 결과적으로 value fn.의 값을 향상하는 격: $v_{\pi’}(s) \ge v_\pi(s)$
- improvement가 멈추면, 결과적으로 아래 식이 성립
- Bellman optimality equation 성립
- 결과적으로 모든 $s \in \mathcal{S}$ 에 대해서, $v_\pi(s) = v_*(s)$ 성립 → $\pi$ 는 최적의 policy로 수렴
Extensions to Policy Iteration
[ Modified Policy Iteration ]
- 문제: policy iteration이 반드시 $v_\pi$ 로 수렴한 뒤에 policy를 결정해야 하는가? (Small Grid World에서도 value fn.이 수렴하지 않았음에도 policy는 수렴함)
- 정지 조건 만들기 (e.g. value fn.에 대해서 $\epsilon$-convergence 적용)
- 단순히 $k$ 번의 반복 이후 종료 (e.g. Small Grid World에서는 $k=3$ 으로 충분했음)
- 해결: policy를 각 반복 스텝마다 업데이트
- 한 스텝마다 policy를 업데이트 하는 것은 결국 value iteration과 동일
- value fn. 관점에서 그저 주어진 policy에 따라 reward를 계산하면 될 뿐임
Value Iteration
Value Iteration in MDPs
[ Principal of Optimality ]
어떠한 최적의 policy라도 아래의 두 요소로 분해 가능
- 최적의 첫 번째 action $A_*$
- 뒤따르는 state $S’$ 의 최적의 policy
(즉, 첫 action을 optimal하게 시작한 이후, 다음 state에서 또 최적의 policy를 찾으면, 최적으로 수렴함)
policy $\pi_(a|s)$ 가 state $s$ 에서 최적의 value $v_\pi(s) = v_*(s)$ 를 달성할 필요충분조건:
- state $s$ 에서 도달 가능한 모든 state $s’$ 에 대해서
- $\pi$ 는 state $s’$ 에서 최적을 달성: $v_\pi(s’) = v_*(s’)$ ($s’$ 에서 최적의 policy에 도달 가능할 때)
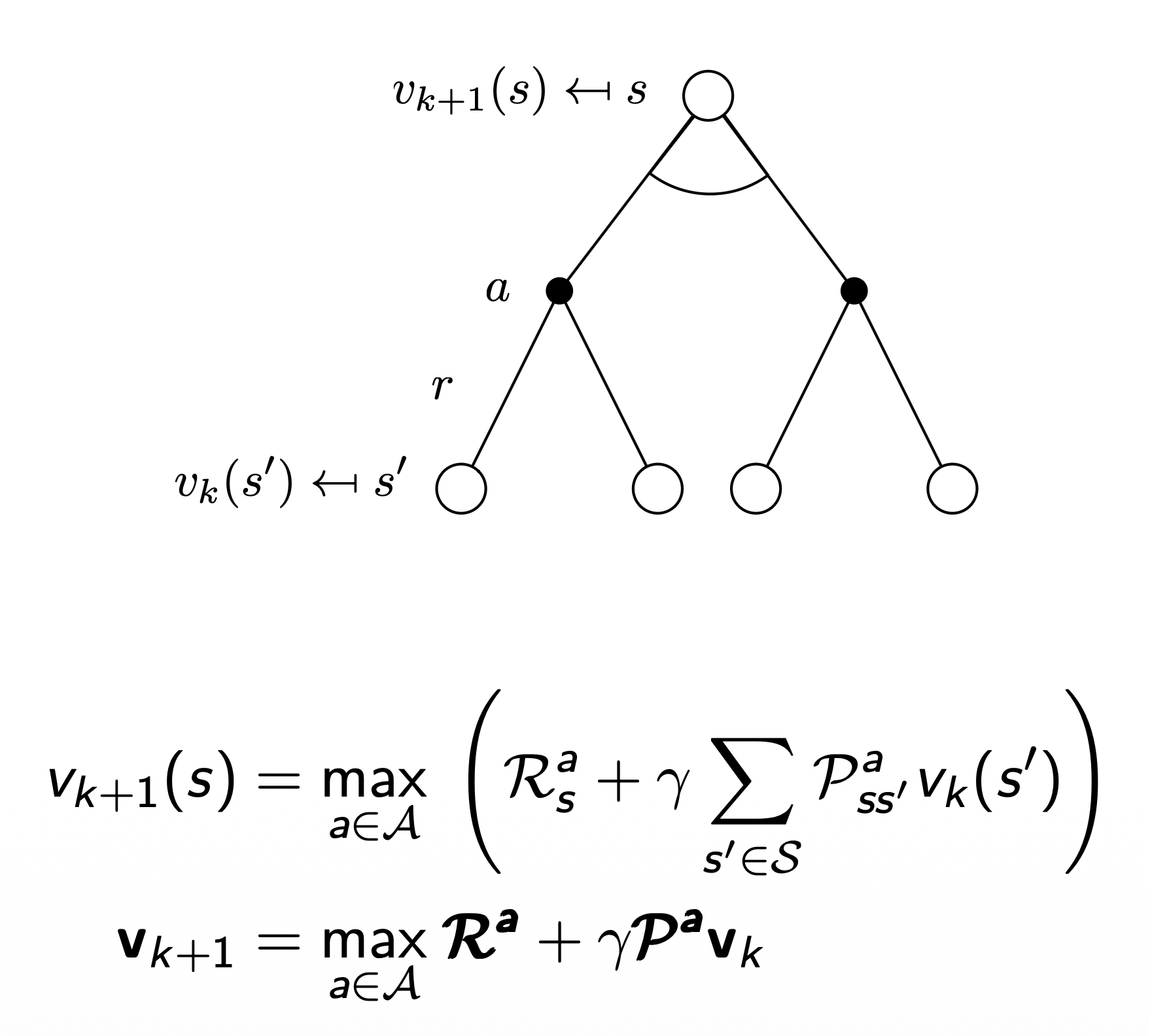
[ Deterministic Value Iteration ]
subproblem의 해인 $v_(s’)$ 을 알고 있으면, 전체 해 $v_(s)$ 는 one-step lookahead로 알 수 있음
- value iteration의 핵심은 위 업데이트를 스텝마다 반복적으로 적용하는 것
- 최종 reward로부터 한 스텝씩 거꾸로 적용하는 직관에서 출발
- loopy MDP, stochastic MDP에도 적용이 가능함
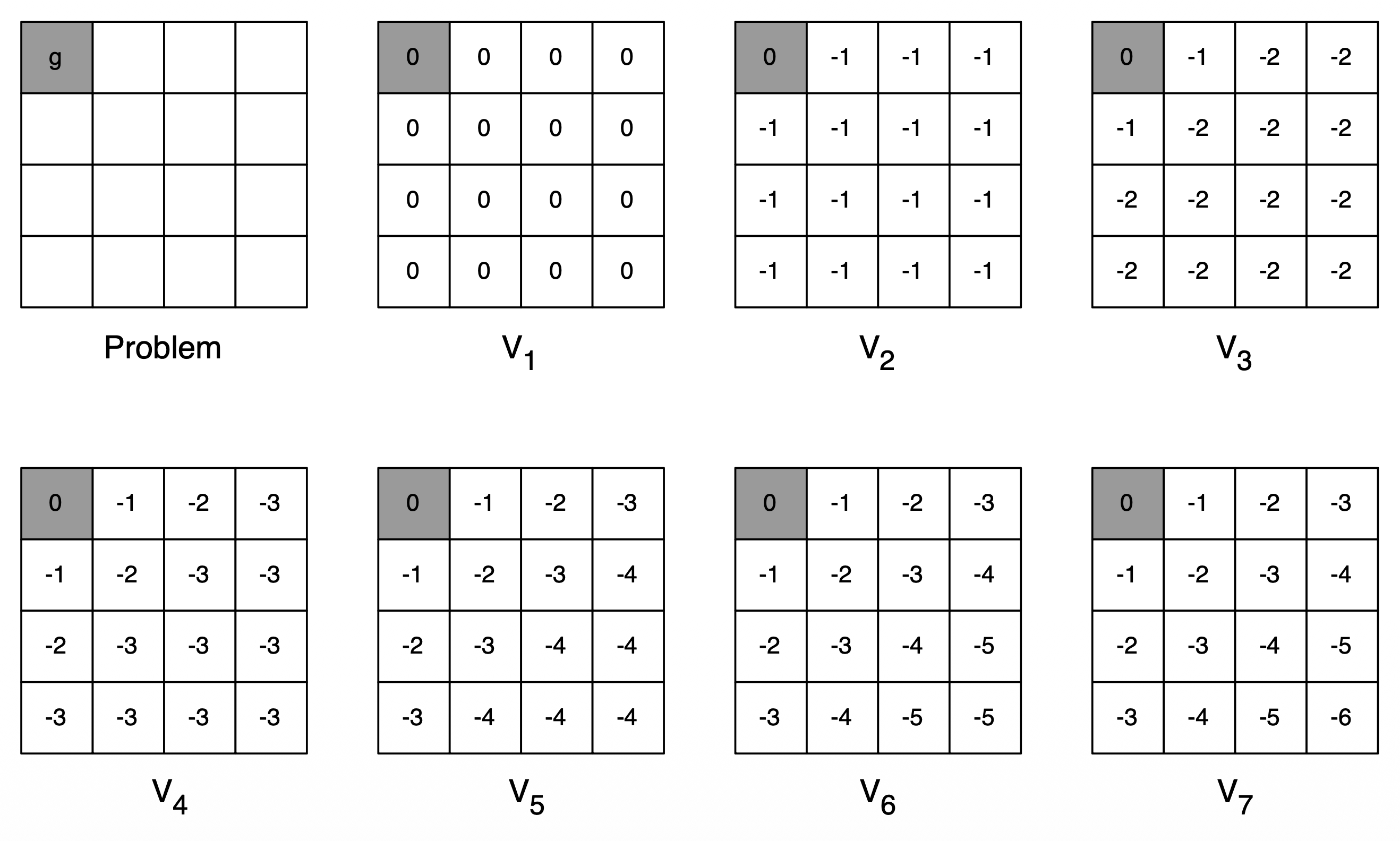
[ Example: Shortest Path ]
- 모든 transition reward는 -1로 가정
- 모든 state의 reward를 one-step lookahead로 계산
- $v_1$ 에서 모든 칸은 0, $v_2$ 에서 모든 칸은 -1인 것이, 한 step에 대해서만 예측하기 때문임
- $v_7$ 이 되어서야 최종적으로 전부 업데이트가 된 상태
[ Value Iteration ]
(Iterative Policy Evaluation과 동일)
Problem
policy $\pi$ 가 주어졌을 때, 해당 policyd의 reward를 계산하는 것
Solution
반복적으로 Bellman Expectation을 적용 ($v_1 \to v_2 \to … \to v_\pi$)
이때, synchronous backups(caching)를 활용 (asynchronous backups는 아직 고려하지 않음)
- 각 iteration step $k+1$ 일 때,
- 모든 state $s \in S$ 에 대해서,
- $v_k(s’)$ 를 활용해서 $v_{k+1}(s)$ 를 업데이트 (이때, $s’$ 은 $s$ 로부터 도달 가능한 다음 state)
- Policy Iteration과의 차이점: $\text{max}$ 가 붙었으며, greedy하게 매 step마다 최적의 value fn.을 찾겠다는 것
Summary of DP Algorithms
[ Synchronous dynamic Programming Algorithms ]
| Problem | Bellman Equation | Algorithm |
|---|---|---|
| Prediction | Bellman Expectation Equation | Iterative Policy Evaluation |
| Control | Bellman Expectation Equation + Greedy Policy Improvement |
Policy Iteration |
| Control | Bellman Optimality Equation | Value Iteration |
- 알고리즘은 state-value function $v_\pi(s)$ 또는 $v_*(s)$ 에 기반함
- $m$ 개의 action, $n$ 개의 state가 있을 때 iteration 마다 시간복잡도: $O(mn^2)$
- 특정 state $s$ 에서 특정 action $a$ 를 수행한다고 할 때, $n$ 개의 state에 대해 synchronous하게 evaluation 수행 → $O(n)$
- 모든 행동 $m$ 개에 대해 해당 evaluation을 동일하게 수행 → $O(mn)$
- 전체 state $n$ 개에 대해 위와 같은 과정을 반복 → $O(mn^2)$
- action-value fn. $q_\pi(s, a)$ 또는 $q_*(s, a)$ 에도 적용 가능
- iteration 마다 시간복잡도: $O(m^2n^2)$
Extensions to Dynamic Programming
Asynchronous Dynamic Programming
- 지금까지의 DP는 synchronous를 기반으로 설명함
- 매 step마다 모든 state가 한 번에 업데이트 됨
- asynchronous DP는 어느 순서에서든 각 state가 독립적으로 업데이트 됨
- 즉, 순서가 전혀 상관 없음
- 선택된 state마다 적절한 backup을 알아서 적용
- 계산량이 현저히 저하됨
- 모든 state가 연속적으로 선택될 수 있다면, 최적으로 수렴이 보장됨
[ 업데이트 할 state를 선택하는 세 가지 방식 ]
- In-place dynamic programming
- Prioritized sweeping
- Real-time dynamic programming
In-Place Dynamic Programming
- synchronous value iteration의 경우, 두 가지 value fn.을 저장해야 함
- 아래 식과 같이 어떤 state $s$ 를 업데이트하기 위해 이전 state의 successor state들에 대해서 sweep하면서 모든 값들을 trajectory에 넣고, 해당 값들을 활용해서 최적의 value fn.으로 업데이트 해야 함
- 결과적으로 old와 new에 대한 두 가지 value fn.을 저장해야 함 ($v_{old} \gets v_{new}$)
$\quad \quad \text{for all} \ s \ \text{in} \ \mathcal{S}$
\[v_{new}(s) \gets \operatorname*{max}\limits_{a \in \mathcal{A}} (\mathcal{R}^a_s + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}^a_{ss'} v_{old}(s')) \\\]- in-place value iteration의 경우, 하나의 value fn.만 저장하면 됨
- 어느 시점에서 업데이트 된 value fn.일지라도 최신의 value fn.로 저장하고, 해당 값을 어느 state에서든 newest value fn.으로 간주하고 사용하는 것
$\quad \quad \text{for all} \ s \ \text{in} \ \mathcal{S}$
\[v(s) \gets \operatorname*{max}\limits_{a \in \mathcal{A}} (\mathcal{R}^a_s + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}^a_{ss'} v(s')) \\\]Prioritized Sweeping
- priority queue를 두고 어떤 state부터 방문하는 것이 좋을지 생각해보자는 아이디어
- Bellman error의 척도를 priority의 기준으로 정함
- 위 식의 값이 가장 큰 state일 수록 업데이트 시 최적으로 도달하는 속도가 빠를 것
- 이전 state의 결과값을 사용하기 때문에 reverse dynamics에 대한 정보가 필요
- 결국 모든 state에 대한 계산값이 필요한 게 아닌가 싶었지만.. 우선 순위의 state $s$ 를 선정해서 점점 좁혀 들어간다고 볼 수 있는 듯함 (아니라면 omg)
Real-Time Dynamic Programming
- 가장 직관적인 방식으로, agent가 real-world에서 실제로 동작하게 한 다음, 직접적으로 영향을 주고받는 state에 대해서만 업데이트를 수행
- 각 timestep에서 $\mathcal{S}t, \mathcal{A}_t, \mathcal{R}{t+1}$ 을 수행한 후, state $\mathcal{S}_t$을 업데이트
Full-Width and Sample Backups
[ Full-Width Backups ]
- DP는 full-width backups를 사용
- sync이든 async이든 간에 각각의 backup은 가능한 모든 state와 action을 전부 고려해서 reward의 기댓값을 계산
- MDP의 전이와 reward fn.을 알아야 함
- 이러한 DP는 너무 크지 않은, 적절한 중간 사이즈(수백만 개의 state)의 문제들에 적합함
- 너무 큰 문제들에 대해서는 Bellman’s curse of dimensionality를 겪게 됨
- state 개수( $n = \mid \mathcal{S} \mid$ )에 따라서 지수적으로 증가
- 단 하나의 backup조차 비용이 클 수 있음
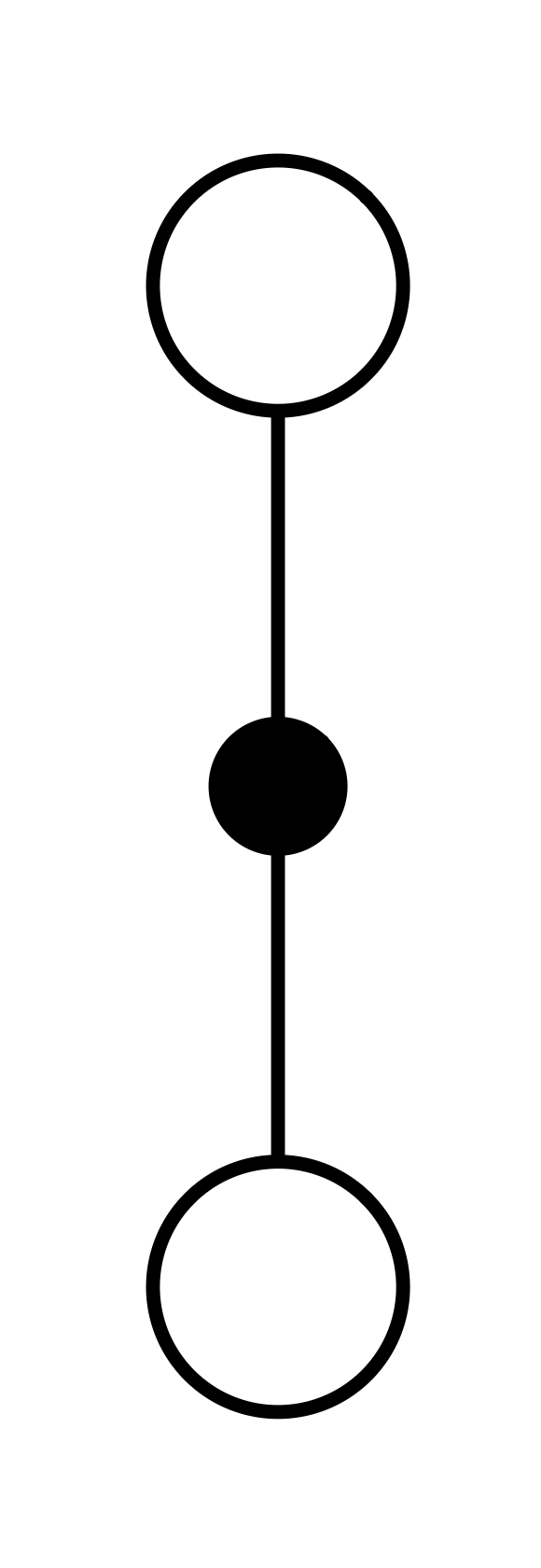
[ Sample backups ]
- reward fn. $\mathcal{R}$ 과 transition dynamics $\mathcal{R}$ 대신에 특정 state와 transition을 샘플링해서 수행 $<\mathsf{S}, \mathsf{A}, \mathsf{R}, \mathsf{S}’>$
- 장점
- model-free: action이든 transition이든 샘플링해서 사용할 것이기 때문에 dynamics를 알려줄 env에 대한 model이 필요없음
- 샘플링하기 때문에 curse of dimensionality 회피 가능
- backup의 비용이 일정함 즉, $n=\mid\mathcal{S}\mid$ 에 독립적
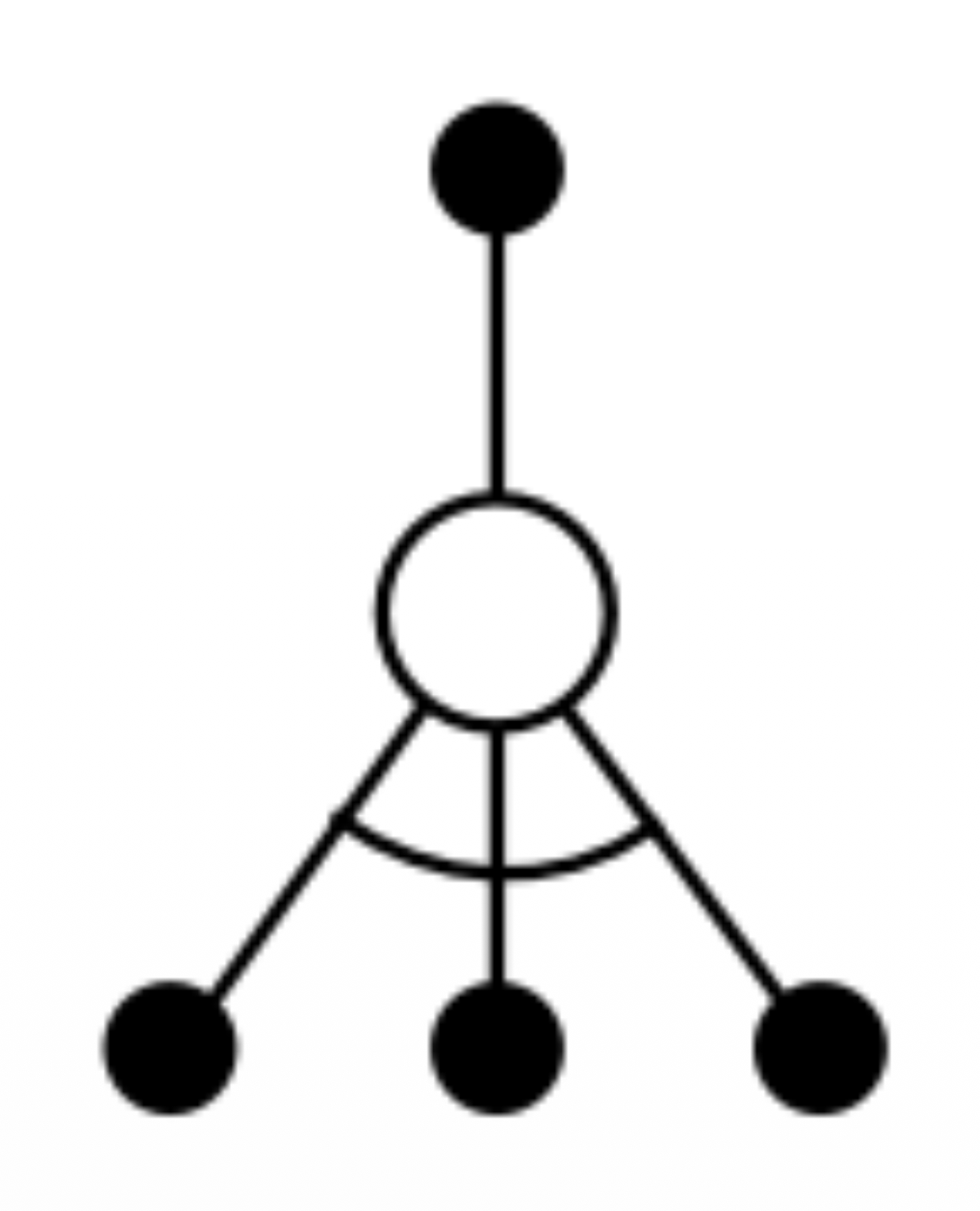
- 왼쪽 (sample backups)
- 어떤 state 하나에서 시작
- policy에 따라 action 하나를 샘플링해서 수행
- dynamics에 따라 하나의 transition을 샘플링
- 이 샘플링 예제에 따라 backup 수행
- 오른쪽 (full-width backups)
- 특정 state에서 실행 가능한 모든 action에 대한 모든 transition을 고려하게 되어있음
Contraction Mapping Theorem
DP를 적용한 RL의 해가 반드시 유일한지, 최적으로 수렴하는 것을 증명
- value iteration to $v_*$
- policy evaluation to $v_\pi$
- therefore, polity iteration to $v_*$
강의에서도 스킵되어 있고, 이해를 못했으므로.. 추후에 공부해보기로!