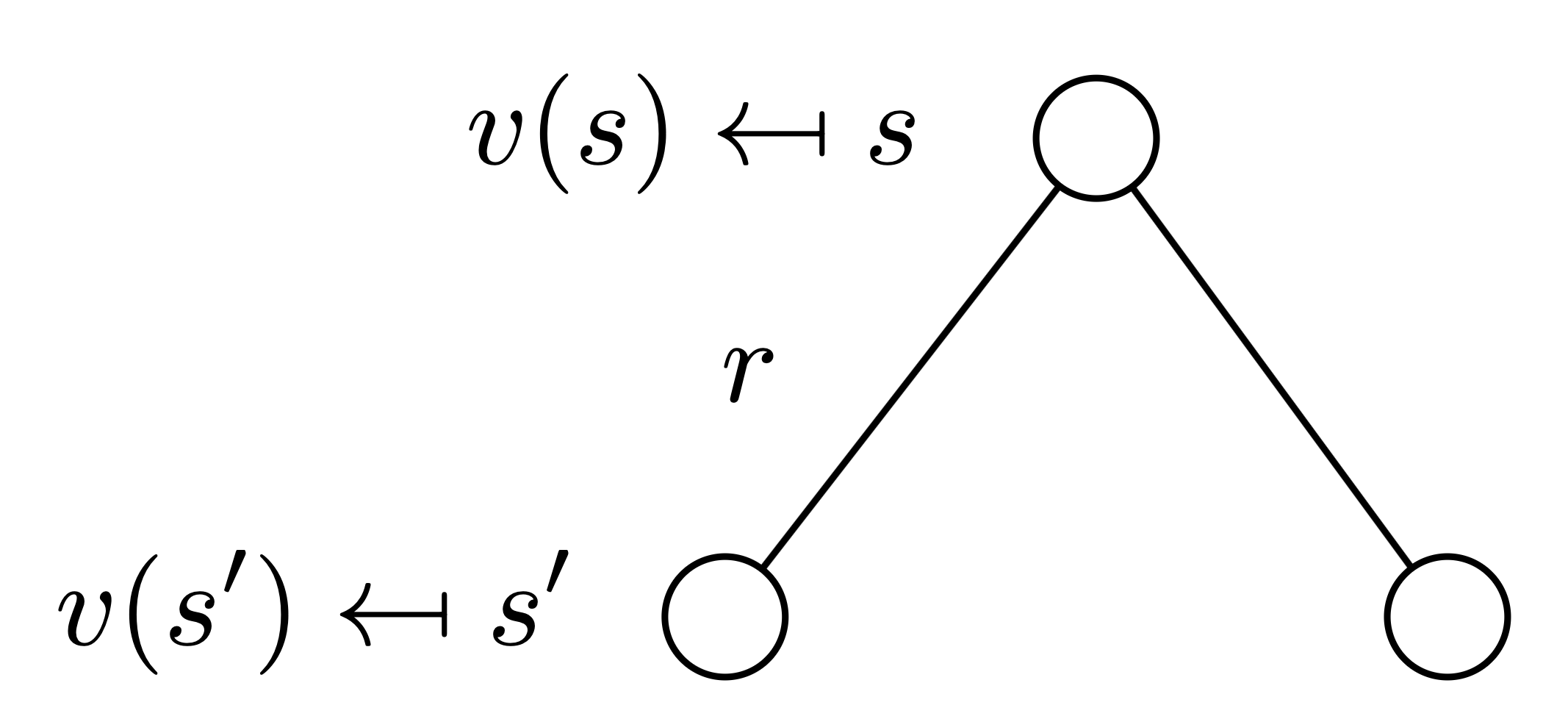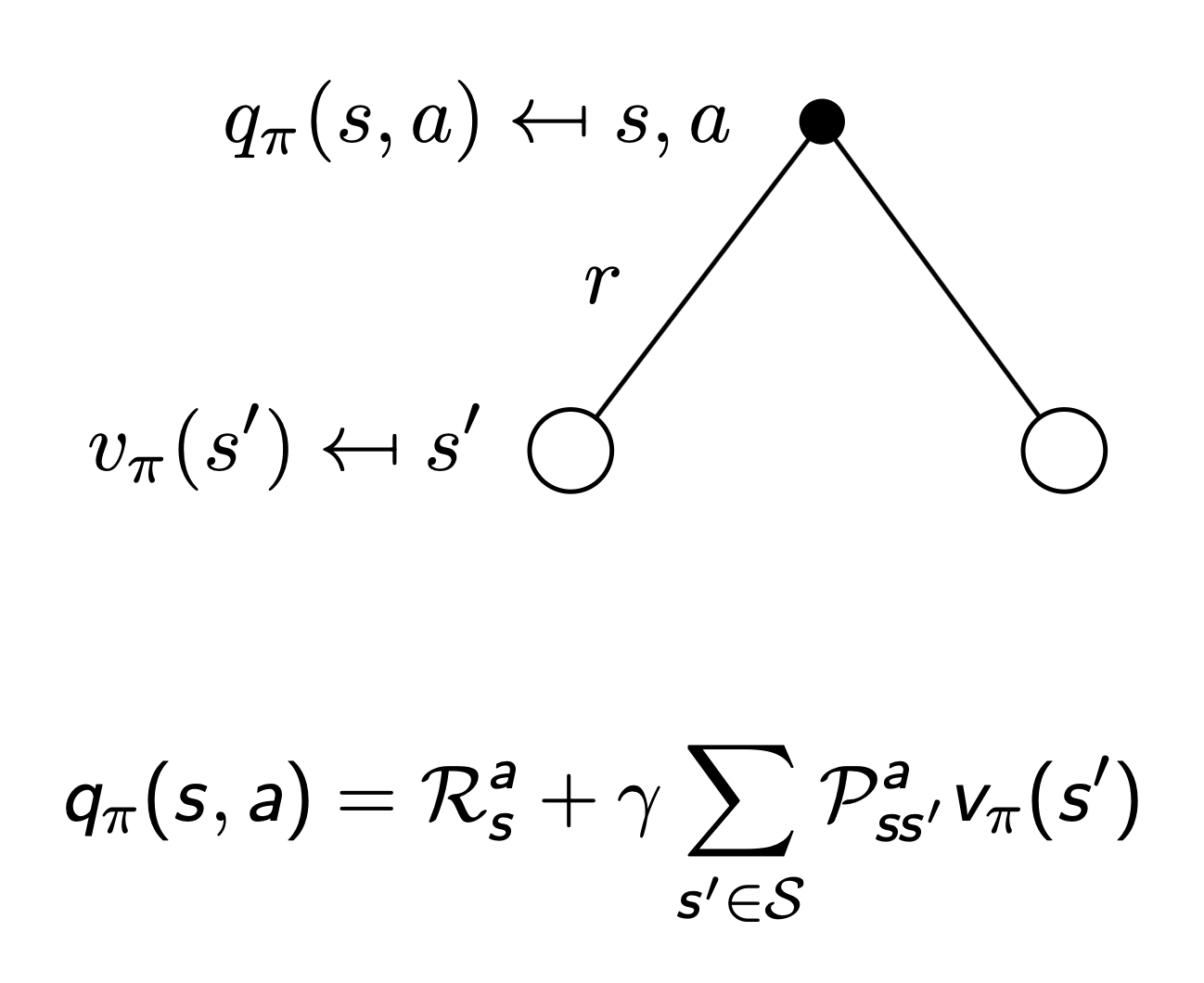Post

Lecture 2. Markov Decision Process

Posted
By oceann
9 min read

이 포스팅은 David Silver의 RL 강좌를 기반으로 작성되었습니다.

Markov Processes

Introduction

  • Markov decision processes는 강화학습에서 environment를 묘사 (where the environment is fully observable)
  • 거의 모든 RL 문제들을 MDP로 표현 가능
    • optimal control은 continuous MDP로 해결
    • partially observable problem도 MDP로 변환해서 해결 가능
    • bandit(action → get feedback)은 state가 하나인 MDP

Markov Property

"The future is independent of the past given the present"

\[\mathbb{P}[S_{t+1}|S_t] = \mathbb{P}[S_{t+1}|S_1,...,S_t]\]
  • state는 history로부터 모든 관련 있는 정보를 포함 → state를 알면, history를 전혀 몰라도 됨
  • The state is sufficient statistic of the future

[ State Transition Matrix ]

\[\mathcal{P}_{SS'} = \mathbb{P}[S_{t+1}=s'|S_t=s]\]
  • $s$: Markov state
  • $s’$: 전이 결과 state
  • $\mathcal{P}$: state 전이 확률
  • 전이 행렬 $\mathcal{P}$ 는 state $s$ 로부터 전이 결과 state $s’$ 으로의 전이 확률을 표현하며, 각 행의 총합은 1
\[\mathcal{P} = \text{from} \begin{bmatrix} \mathcal{P}_{11} ... \mathcal{P}_{1n} \\ ... \\ \mathcal{P}_{n1} ... \mathcal{P}_{nn} \end{bmatrix}\]

Markov Chains

[ Markov Process ]
이 자체로 강화학습을 수행하는 것이 아니라, 어떤 state가 Markov Property를 만족하는 프로세스에 대한 정의
Markov Process (or Markov Chain) 튜플 $<\mathcal{S}, \mathcal{P}>$ 에 대하여

  • $\mathcal{S}$: state들의 유한 집합
  • $\mathcal{P}$: state 전이 확률 행렬
\[\mathcal{P}_{ss'} = \mathbb{P}[S_{t+1}=s' \mid S_{t}=s]\]

(+ sample: 특정 state에서 terminate/goal state까지의 sequence)

Markov Reward Processes

MP에서 value(가치)를 추가한 프로세스
Markov Process (or Markov Chain) 튜플 $<\mathcal{S}, \mathcal{P}, \mathcal{R}, \gamma>$ 에 대하여

  • $\mathcal{S}$: state들의 유한 집합
  • $\mathcal{P}$: state 전이 확률 행렬
\[\mathcal{P}_{ss'} = \mathbb{P}[S_{t+1}=s' \mid S_{t}=s]\]
  • $\mathcal{R}$: reward 함수
\[\mathcal{R}_s = \mathbb{E}[R_{t+1}|S_t=s]\]
  • $\gamma$: discount factor (시간적 요소를 반영), $\gamma \in [0, 1]$

Return

time-step $t$에서 얻을 수 있는 모든 할인(by discount factor)된 reward의 총합

\[G_t = R_{t+1} + \gamma R_{t+2} + ... = \sum_{k=0}^{\infty}\gamma^kR_{t+k+1}\]
  • $\gamma$는 미래 reward에 대한 현재의 값
  • 현재 timestep에서 지연된 reward들에 대해 즉각적인 reward를 구할 수 있음
    • $\gamma \to 0$: “myopic” 평가
    • $\gamma \to 1$: “far-sighted” 평가

Why Discount?

  • 수학적 편의성 (수렴)
  • cyclic MP에서의 무한 루프 회피
  • 미래에 대한 불확실성: reward를 예측하는 model이 불완전할 수 있기 때문에 timestep이 멀어질 수록 불확실성이 커짐
  • reward가 금전적인 문제와 관련이 있다면, 미래보다 즉시 받을 수 있는 reward가 더 가치있음
  • 동물/사람은 즉각적인 reward에 더 크게 반응 (agent를 cognitive model처럼 생각)
  • 모든 sequence에 대해 종료 조건이 존재한다면 $\gamma=1$ 사용도 가능

Value Function

MRP에서 value 함수 $v(s)$ 는 state $s$ 로부터의 return에 대한 기댓값을 제공

\[v(s) = \mathbb{E}[G_t | S_t=s]\]
  • goal state까지만이 아니라 미래에 받을 수 있는 모든 누적 보상
  • 기댓값인 이유: environment가 stochastic
  • $v(s)$ 자체는 maxmize의 개념이 없고, agent의 action에 따라 $v(s)$ 를 통해 구한 reward를 최대화하는 것이 목표

Bellman Equation for MRPs

value 함수는 두 개의 요소로 분해 가능: 즉각적인 reward $R_{t+1}$, 다음 state에서 얻을 보상인 $\gamma v(S_{t+1})$

\[v(s) = \mathbb{E}[G_t | S_t=s] \\ = \mathbb{E}[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... | S_t=s] \\ = \mathbb{E}[R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + ...) | S_t=s] \\ = \mathbb{E}[R_{t+1} + \gamma G_{t+1} | S_t=s] \\ = \mathbb{E}[R_{t+1} + \gamma v(S_{t+1}) | S_t=s] \\\]
  • 엣지가 한 개인 트리로 표현 가능
\[v(s) = \mathcal{R}_s + \gamma \sum_{s' \in S}\mathcal{P}_{ss'}v(s')\]

[ Bellman Equation in Matrix Form ]

\[v = \mathcal{R} + \gamma \mathcal{P}v\]
  • $v$ 는 각 요소가 state에 해당하는 열벡터
\[\begin{bmatrix} v(1) \\ ... \\ v(n) \end{bmatrix} = \begin{bmatrix} \mathcal{R}_1 \\ ... \\ \mathcal{R}_n \end{bmatrix} + \gamma \begin{bmatrix} \mathcal{P}_{11} ... \mathcal{P}_{1n} \\ ... \\ \mathcal{P}_{1n} ... \mathcal{P}_{nn} \end{bmatrix} \begin{bmatrix} v(1) \\ ... \\ v(n) \end{bmatrix}\]

[ Solving the Bellman Equation ]

  • Bellman Equation은 선형식이기 때문에 아래와 같이 해결 가능
\[v = \mathcal{R} + \gamma \mathcal{P}v \\ (I-\gamma \mathcal{P})v = \mathcal{R} \\ v = (I-\gamma \mathcal{P})^{-1}\mathcal{R}\]
  • $n$ 개의 state들에 대한 시간 복잡도는 $O(n^3)$ → $n$ 이 너무 커지면 오래 걸릴 수 있음
  • 역행렬이 존재해야 함
  • 매우 큰 $n$ 에 대해서 반복적으로 접근하는 방식
    • dynamic programming
    • monte-carlo evaluation
    • temporal-difference learning

Markov Decision Processes

MRP에서 결정의 개념을 추가한 프로세스로, 결정이 가능한 상황에서 agent가 action을 수행할 수 있음 (당연히 모든 state가 Markov)
Markov Decision Process 튜플 $<\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma>$ 에 대하여

  • $\mathcal{S}$: state들의 유한 집합
  • $\mathcal{A}$: action들의 유한 집합
  • $\mathcal{P}$: state 전이 확률 행렬
\[\mathcal{P}_{ss'}^a = \mathbb{P}[S_{t+1}=s' \mid S_{t}=s, \mid A_t=a]\]
  • $\mathcal{R}$: reward 함수
\[\mathcal{R}_s^a = \mathbb{E}[R_{t+1}|S_t=s, A_t=a]\]
  • $\gamma$: discount factor (시간적 요소를 반영), $\gamma \in [0, 1]$

Policies

state가 주어졌을 때 action에 대한 분포

\[\pi (a|s) = \mathbb{P}[A_t=a|s_t=s]\]
  • policy는 agent의 행동을 완전하게 정의
  • MDP의 policy는 현재 state에 의존 (history가 아니라 $\because$ Markov)
  • policy는 stationary (시간에 독립적) $\because$ Markov이기 때문에 현재 state만 확인하면 됨
    $A_t~\pi (\cdot | S_t), \forall t > 0$
  • 주어진 MDP $\mathcal{M} = <\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma>$와 policy $\pi$ 에 대해서
    • state들의 시퀀스 $S_1, S_2, …$ 는 Markov process $<\mathcal{S}, \mathcal{P}^\pi>$
    • state와 reward들의 시퀀스 $S_1, R_2, S_2, …$ 는 Markov reward process $<\mathcal{S}, \mathcal{P}^\pi, \mathcal{R}^\pi, \gamma>$ 이며, $\mathcal{P}$ 와 $\mathcal{R}$ 은 아래를 따름
\[\mathcal{P}^\pi_{S, S'} = \sum_{a \in \mathcal{A}}\pi(a|s)\mathcal{P}^a_{SS'} \\ \mathcal{R}^\pi_S = \sum_{a \in \mathcal{A}}\pi(a|s)\mathcal{R}^a_{S}\]

Value Function

MDP에서의 state-value function이란, state s에서 뒤따르는 policy pi에 대해 return에 대한 기댓값

\[v_\pi(s) = \mathbb{E}_\pi[G_t | S_t = s]\]

MDP에서의 action-value function이란, agent가 state s에서 action a를 취했을 때, 뒤따르는 policy pi에 대해 return에 대한 기댓값

\[q_\pi(s,a) = \mathbb{E}[G_t | S_t=s, A_t=a]\]

Bellman Expectation Equation

  • 즉시 받을 수 있는 reward와 다음 state에서의 reward의 합으로 표현 가능

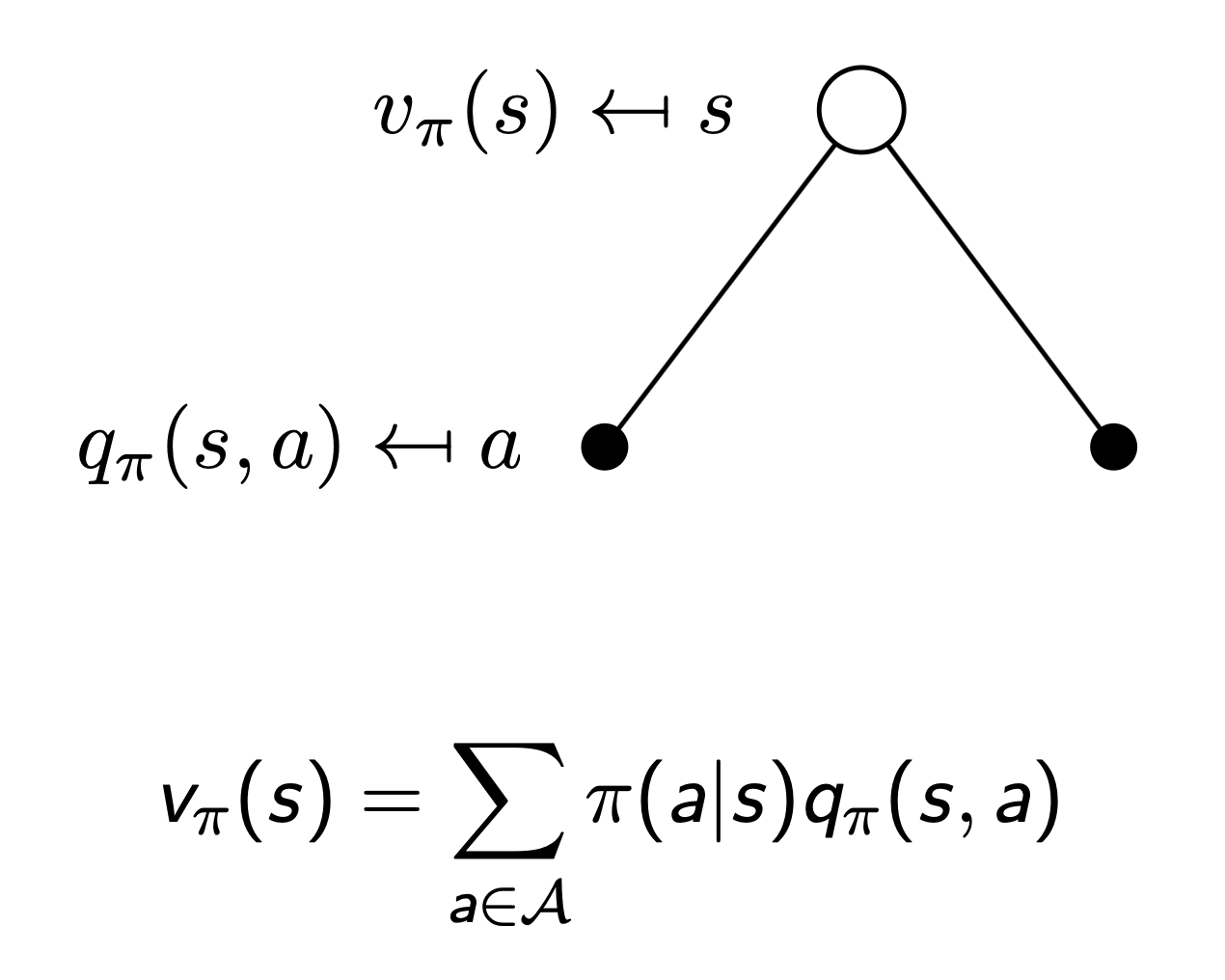
state-value function

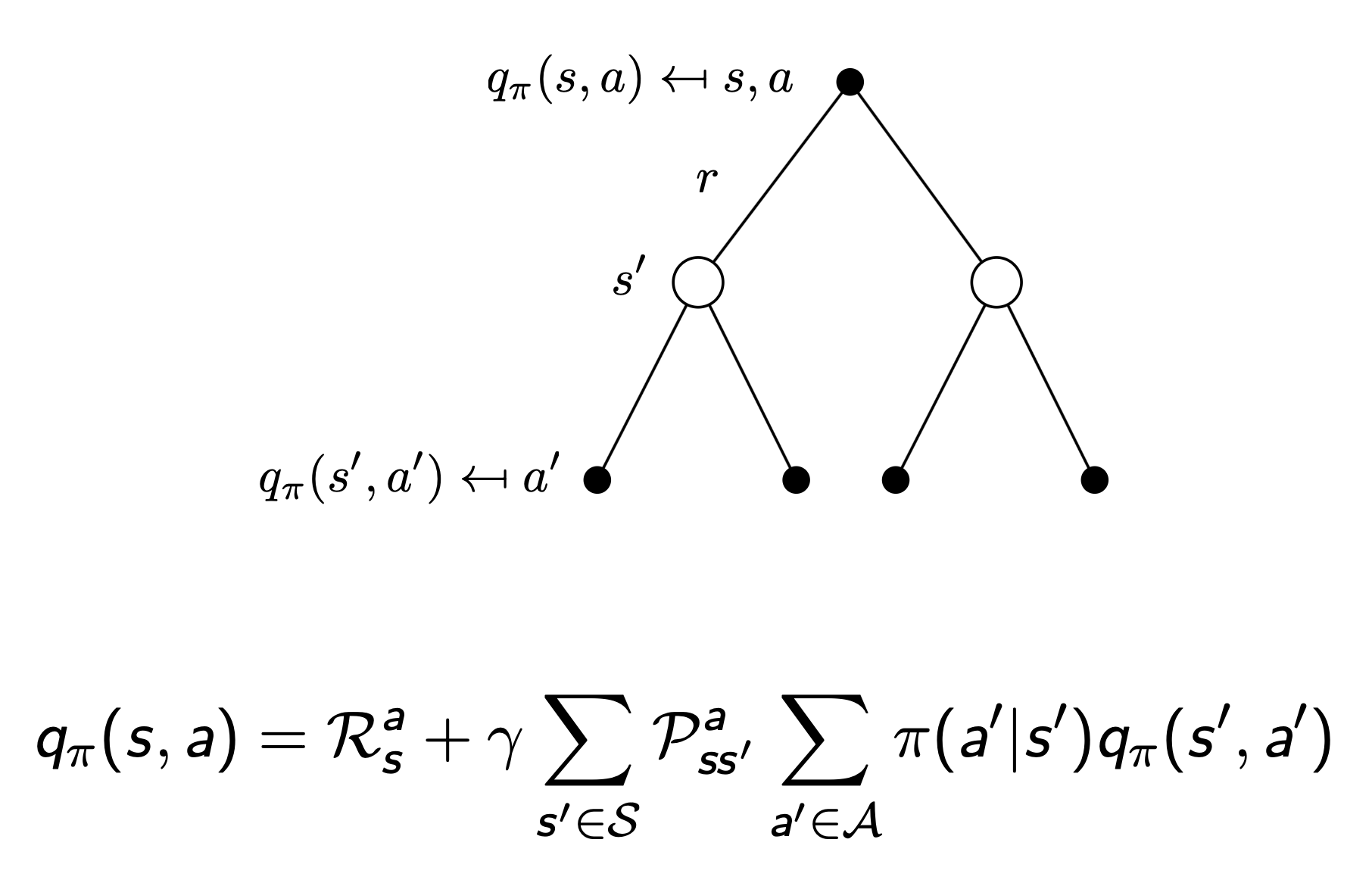
\[v_\pi(s) = \mathbb{E}_\pi[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t = s]\]

action-value function

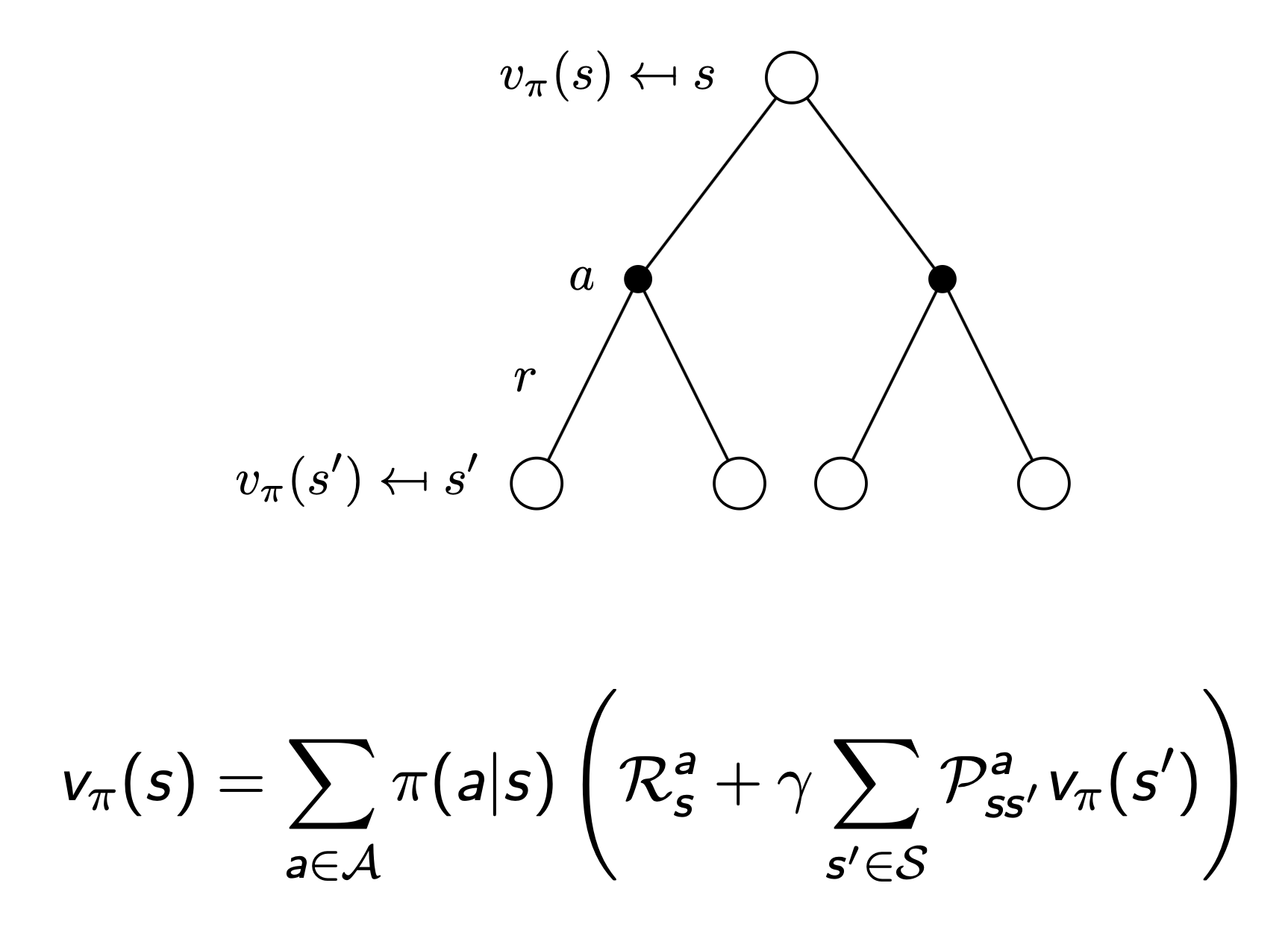
\[q_\pi(s,a) = \mathbb{E}[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) | S_t=s, A_t=a]\]
  • two step state-value & action-value function
    • value의 action reward에 action-value function을 적용
    • action의 state reward에 state-value function을 적용

Optimal Value Function

optimal state-value function이란, 모든 policy 중에서 기댓값이 최대가 되는 경우의 value function

\[v_*(s) = \max_\pi v_\pi(s)\]

optimal action-value function이란, 모든 policy 중에서 기댓값이 최대가 되는 경우의 action-value function

\[q_*(s, a) = \max_\pi q_\pi(s, a)\]
  • MDP는 최적의 value fn.을 찾았을 때 비로소 “해결”됨

Optimal Policy

\[\pi \ge \pi' \ \text{if} \ v_\pi(s) \ge v_{\pi'}(s), \forall s\]
  • 모든 MDP에 대해서 이론적으로
    • 다른 모든 policy $\pi$ 와 같거나, 더 나은 policy $\pi_*$ 가 반드시 존재
    • 모든 최적의 policy들은 최적의 value fn.을 만족 → $v_{\pi_}(s) = v_(s)$
    • 모든 최적의 policy들은 최적의 action-value fn.을 만족 → $q_{\pi_}(s, a) = q_(s, a)$
  • $q_*(s, a)$ 를 최대화 함으로써 최적의 policy를 찾을 수 있음
    • 즉, $q_*(s, a)$ 를 알면 최적의 policy를 찾은 것과 마찬가지
\[\pi^{*}(a \mid s) = \begin{cases} 1 & \text{if } a = \arg\max\limits_{a \in \mathcal{A}} q^{*}(s, a) \\ 0 & \text{otherwise} \end{cases}\]
  • Bellman eq.을 적용해서 동일하게 recursive한 방식으로 해결 가능

Solving the Bellman Optimality Equation

  • Bellman Optimality Equation은 비선형적이며, 일반적으로 closed form solution이 없음
  • 다양한 iterative 방식을 적용
    • Value Iteration
    • Policy Iteration
    • Q-learning
    • Sarsa
RL, David Silver
RL
This post is licensed under CC BY 4.0 by the author.