Post

Language Models Resist Alignment, Evidence from Data Compression

Posted
By oceann
31 min read

[ 개요 ]

  • 의의: 사전 학습된 언어 모델들에 post training을 할 때, 데이터의 크기와 분포에 따라 tuning의 목적을 잘 따르지 않는 경향(misalignment)을 확인
    • 모델의 성능과 동치인 데이터 압축률(compression rate)을 통해 수식적으로 설명
    • 벤치마크 데이터셋들을 활용해서 실험적으로 설명
  • 한계: 모델의 성능과 compression rate이 동치임을 설명한 내용과 실험 간의 alignment가 빈약함 (최하단 comment 참고)

Introduction

  • 현대에는 언어 모델들이 뛰어난 성능을 보여주고 있는 반면, 학습 데이터셋의 편향, 위험한 요소 등이 불가피하게 포함되어 있기 때문에 인간의 의도와는 다른 출력을 낼 때가 존재
  • 이를 개선하기 위해 supervised fine-tuning (SFT), reinforcement learning with human feedback (RLHF) 등의 기법들이 적용되고 있음
  • 하지만 해당 기법들은 모델 전체를 통제하지 못하고 사전 학습의 분포에 머물러 있거나, 되돌아가려는 성질을 가져 결과적으로 misalignment를 야기함
  • 이를 모델의 탄성(elasticity)이라 부르며 데이터 압축률(compression rate)의 개념을 활용하여 설명함

What is Elasticity

해당 파트에서는 LM의 성능을 데이터 압축률, LM의 성질을 elasticity로 설명하고, elasticity를 활용해서 모델의 데이터 압축을 설명함
어려워서 생략한 수식들과 증명들이 있는데, 이해 가능한 선에서, 또한 논문을 이해할 수 있는 선에서 최대한 서술해봄

[ Preliminaries ]
elasticity alignment를 거부하고 원래의 분포로 되돌아가려는 성질

Compression Rate

  • 정보 이론에 근거하여 중요한 정보일 수록 적은 비트수를 할당하여 정보의 최대 압축률을 달성하는 것이 목적
    • 자주 발생하는 정보에 낮은 비트수를 할당, 전체 정보에 해당하는 총 비트수의 크기를 작게 유지
    • 특정 정보에 할당된 비트수가 곧 소스 코드의 길이, 엔트로피를 의미함
    • “엔트로피가 낮을 수록 정보의 중요도가 작다” ex. 해는 동쪽에서 뜬다 (당연하기 때문에 정보량 적음, 더 적은 비트수를 할당) vs. 내일 NVIDIA의 주식이 상승할 것이다 (모르기 때문에 정보량 높음, 더 많은 비트수를 할당)
  • Shannon’s source coding theorem을 이용하며 언어 모델의 학습 과정에서 Cross Entropy Loss를 줄여나가 최종적으로 얻은 Cross Entropy가 정보의 압축률과 동일함
  • 정리: LLM의 관점에서 Next Token Prediction을 수행할 때, 모델의 성능이 높다는 것은 정답에 해당하는 토큰의 확률이 가장 높다는 것 = 확률이 높다는 것은 당연한 정보라는 것 = 더 적은 엔트로피를 필요로 한다는 것 = 더 적은 엔트로피라는 것은 필요한 비트수가 적다는 것 = 최종적으로 압축률이 높은 것

[ The Compression Protocol of LLMs ]

  • 모델의 성능과 압축률이 동치이기 때문에 LLM의 데이터 압축 프로토콜을 해당 정의에 근거하여 설명하는 파트

Definition 3.1 (Token Tree $\tau$)
데이터셋 $\mathcal{D} = \lbrace z_i, \in \lbrace 0 \mid 1 \rbrace^\infty \mid i=1,2, \dots \rbrace$ 에 대하여, $\mathcal{D}$ 의 토큰 트리는 $\tau_{\mathcal{D}}$ 라고 표기하고, 다음과 같이 정의한다: 각 노드는 0 또는 1로 레이블된 자식 노드를 가지며, 그 끝에는 end-of-sequence (EOS)를 리프 노드로 가진다. 루트 노드로부터 리프 노드까지의 경로 각각은 응답 $z_i$ 에 해당하고, 해당 EOS 노드의 가중치가 곧 해당 응답의 확률이 되며, 리프 노드가 없는 경우에는 모든 자식 노드들이 가진 가중치의 합이 확률이 된다.

1
2
3

즉, 데이터셋의 각 데이터를 Next Token Prediction 관점에서 트리 형태로 형상화하고,
각 경로의 가중치에 대한 값들을 해당 데이터의 확률로 본다는 것이다. 
결과적으로 모델의 학습 과정이란 데이터셋의 토큰 트리의 노드별 가중치들을 학습하는 것이라고 볼 수 있다.
  • 하지만 임의의 깊이를 가진 트리의 노드들을 정확히 캡쳐하기 어렵기 때문에 다음을 가정한다.

Assumption 3.2 (Scale of $\tau$ is Monotone with Model Size)
모델 $p_\theta$ 와 데이터셋 $\mathcal{D}$ 에 대해서, $p_\theta$ 가 완벽히 모델링 할 수 있는 $\tau_{\mathcal{D}}$ 의 일부의 깊이는 파라미터 크기 $\theta$ 에 따라 단조 증가한다.

1
2

즉, 모델이 학습할 수 있는 token tree의 고정 깊이는 모델의 크기에 좌우된다는 것이다.
이를 바탕으로 아래 정의가 도출된다.

Definition 3.3 (The Compression Protocol)
모델 $p_\theta(\cdot)$ 을 사용해서 데이터셋 $\mathcal{D}$ 를 압축하는 상황을 고려해보자. 압축률은 두 단계로 정의된다: a) $\mathcal{D}$ 의 토큰 트리를 잘라내고 상위 $d$ 개의 레이어들만 남긴다. b) Huffman 코딩을 적용해서 잘린 토큰 트리를 압축한다. 구체적으로, 루트 노트로부터 리프 노드까지의 응답은 Huffman 코딩 알파벳을 상징하고, 각 리프 노드의 가중치는 해당 상징에 대한 확률이다.

1
2
3
4

Huffman 코딩은 대표적인 무손실 압축 알고리즘 중 하나이며,
빈도 수가 높은 데이터에 짧은 코드를 부여하고, 반대로 낮은 데이터에 긴 코드를 부여한다.
따라서 해당 방식을 통한 데이터 압축은 최적의 압축을 보장하며,
모델의 이상적인 코드 길이는 다음과 같이 계산될 수 있다.

Theorem 3.4 (Ideal Code Length)
모델 $p_\theta(\cdot)$ 이 데이터셋 $\mathcal{D}$ 를 학습하는 과정에서, 임의의 답변 $x$ 를 압축한 코드 길이 $\mathcal{L}{p\theta}(x)$ 는 다음과 같이 표현될 수 있다:

\[\mathbb{E}[\mathcal{L}_{p_\theta}(x)] = \Biggl\lceil \frac{\mid x \mid}{d} \Biggl\rceil \Biggl\lceil -\sum^d_{l=1}\sum^{2^{l-1}}_{j=1}p_{lj}\log p_{lj} \Biggl\rceil\]

$d$ 는 Definition 3.3에 따라 $\tau_{\mathcal{D}}$ 를 잘라낸 깊이를 의미하고, $p_{lj}$ 는 $l$ 번째 깊이의 $j$ 번째 노드에 해당하는 리프 노드의 확률값을 의미한다.

  • 해당 이론에 더불어, 학습과 alignment는 서로 다른 독립적인 분포를 따르는 여러 개의 데이터셋을 포함할 수 있기 때문에 아래와 같은 정규화된 압축률을 계산
\[p_{lj}^{\mathcal{D}} = \frac{\Sigma^N_{i=1}p_l^{D_i} \mid \mathcal{D}_i \mid}{\Sigma^N_{i=1} \mid \mathcal{D}_i \mid}\]
  • 결과적으로 특정 데이터셋 $\mathcal{D_i}$ 에 대한 압축률 $\gamma_{p_\theta}^{\mathcal{D_i}}$ 는 다음과 같이 정의됨
\[\gamma^{\mathcal{D}_i}_{p_\theta} = \mathbb{E}_{x \sim \mathcal{P}_i} \Biggl[ \frac{\mathbb{E}_{x \sim \mathcal{P}_i} [\mathcal{L}_{p_\theta}^{\mathcal{D}_i}(x)]}{\mid x \mid} \Biggl] \\ = \Theta \Biggl(- \frac{\Sigma^d_{l=1} \Sigma^{2^{l-1}}_{j=1}p_{lj}^{\mathcal{D_i}}\log p^{\mathcal{D}}_{p_{lj}}}{d} \Biggl)\]

[ The Formal Definition of Elasticity ]

  • 해당 파트에서는 모델의 데이터 분포 비교를 통해 elasticity를 설명함
  • 분포 비교를 위해 데이터 압축률의 개념이 사용됨

Definition 3.6 (The Elasticity of LLMs)
변환 $p_{\theta_0} \xrightarrow{\, f(D_a)\,} p_{\theta_1}$ 에 대해서, 어떤 단순한 inverse operation $g$ 와 데이터셋 $\mathcal{D_b}$ 가 있을 때, $(p_{\theta_0}, \mathcal{D_a})$ 사이에 elasticity가 존재한다. 이때, $|\mathcal{D_b}| \ll |\mathcal{D_a}|$ 이다.

\[p_{\theta_0} \xrightarrow{\, g(D_b)\,} p_{\theta'_0} \ \text{and} \ \rho(p_{\theta'_0}, p_{\theta_0}) \leq \epsilon_0.\]
  • $p_{\theta_0}$: pre-trained model
  • $f$, $g$: fine-tuning과 같은 post training을 의미하는 변환 함수
  • $\rho$: 두 분포의 유사도를 측정하는 단순한 함수, 본 논문에서는 압축률을 사용함
  • $\epsilon_0$: 고정 상수로, 두 분포의 유사도가 해당 값 이하면 동일 분포라고 가정함
1
2

즉, 사전 학습 모델에 대한 fine-tuning 이후 작은 크기의 데이터셋으로 추가 학습(perturbation)을 수행하면,
최종 학습 이후의 모델의 분포가 기존의 사전 학습 분포로 근사한다.

Why Elasticity Affects Alignment

  • 해당 파트에서는 모델의 학습과 alignment 과정에서 발생하는 resistance의 이유를 elasticity로 설명

[ Formal Derivation of Elasticity ]

TeX 문법 수식 렌더링이 안 돼서 직접 정리한 캡쳐본으로 대체 ㅠㅠ

1
2
3
4
5

즉, perturbation이 증가할 수록, 사전 학습 모델에 대한 정규화된 압축률은 감소하고,
alignment 데이터셋에 대한 정규화된 압축률은 증가한다.
이때, Pareto mass distribution을 따른다고 가정했기 때문에, 모델이 보다 큰 크기의 데이터셋(pre-train 데이터셋)의 분포를 따르게 되고,
비교적 작은 크기의 alignment 데이터셋과 perturbation 데이터셋의 효과는 거의 없음을 알 수 있다.
(Pareto mass distribution: 상위 소수 패턴이 압축률에 지배적으로 기여하며, 강도가 작은 꼬리 쪽은 길게 퍼짐)

[ Elasticity and Hooke’s Law ]

  • 학습된 모델은 elasticity를 가지며, 앞서 설명한 Theorem 4.2에 의해 그 크기는 데이터셋의 크기에 반비례
  • 특히, 작은 크기의 데이터셋 $\mathcal{D}_t$ 를 사용한 perturbation이 발생했을 때 모델의 분포에 우위를 차지하는 사전 학습 데이터셋 $\mathcal{D}_p$ 의 분포로 로 수렴하는 경향이 있음
  • 이렇게 원래의 형태(사전 학습 모델의 분포)로 되돌아가려는 성질을 용수철 상수를 사용한 Hooke’s Law에 빗대어 표현
\[F \propto k_i \cdot \Delta l_1 = k_2 \cdot \Delta l_2 \\ F \propto \mid \mathcal{D}_i \mid \cdot \Delta \mathcal{D}_{\text{KL}}(\mathcal{P}_{p_\theta} \mid\mid \mathcal{P}_{\mathcal{D}_i})\]
  • $\Delta \mathcal{D_{\text{KL}}}$ : fine-tuning 하기 전 모델 $p_{\theta}$ 의 분포와 데이터셋 $\mathcal{D_i}$ 의 분포의 KL-divergence와 fine-tuning 한 이후의 모델 $p_{\theta}$ 의 분포와 데이터셋 $\mathcal{D_i}$ 의 분포의 KL-divergence에 대한 변화량
  • 즉, 튜닝을 수행한 이후에, 기존에 학습된 모델의 데이터셋의 크기가 클수록 해당 데이터셋과의 분포 차이가 적음
  • Ex. pre-train ($\mathcal{D}_p$) → SFT 1 ($\mathcal{D}_1$) → SFT 2 ($\mathcal{D}_2$) 를 가정했을 때, pre-train만 수행한 모델과 $\mathcal{D}_p$ 의 분포 차이와 SFT 2까지 수행한 이후의 모델과 $\mathcal{D}_p$ 의 분포 차이는 $\mathcal{D}_1$ 과의 차이보다 작다는 것을 의미

Experiments

elasticity와 관련하여 모델의 두 가지 특징을 주장하며, 실험적으로 증명

Resistance for Pre-Trained Models 사전 학습 모델은 fine-tuning 시 alignment를 거부하고 기존의 분포를 유지하려는 경향
Rebound for Post-Trained Models 사전 학습과 사후 학습을 거친 모델에 대해 역방향으로 fine-tuning (e.g., safe vs. unsafe)을 할 경우, 사전 학습 분포로 재빠르게 되돌아오려는 경향

[ Existence of Language Models’ Resistence ]

  • 실험 설계
    • forward alignment보다 inverse alignment보다 쉽다는 것을 통해 사전 학습된 모델의 resistance를 증명
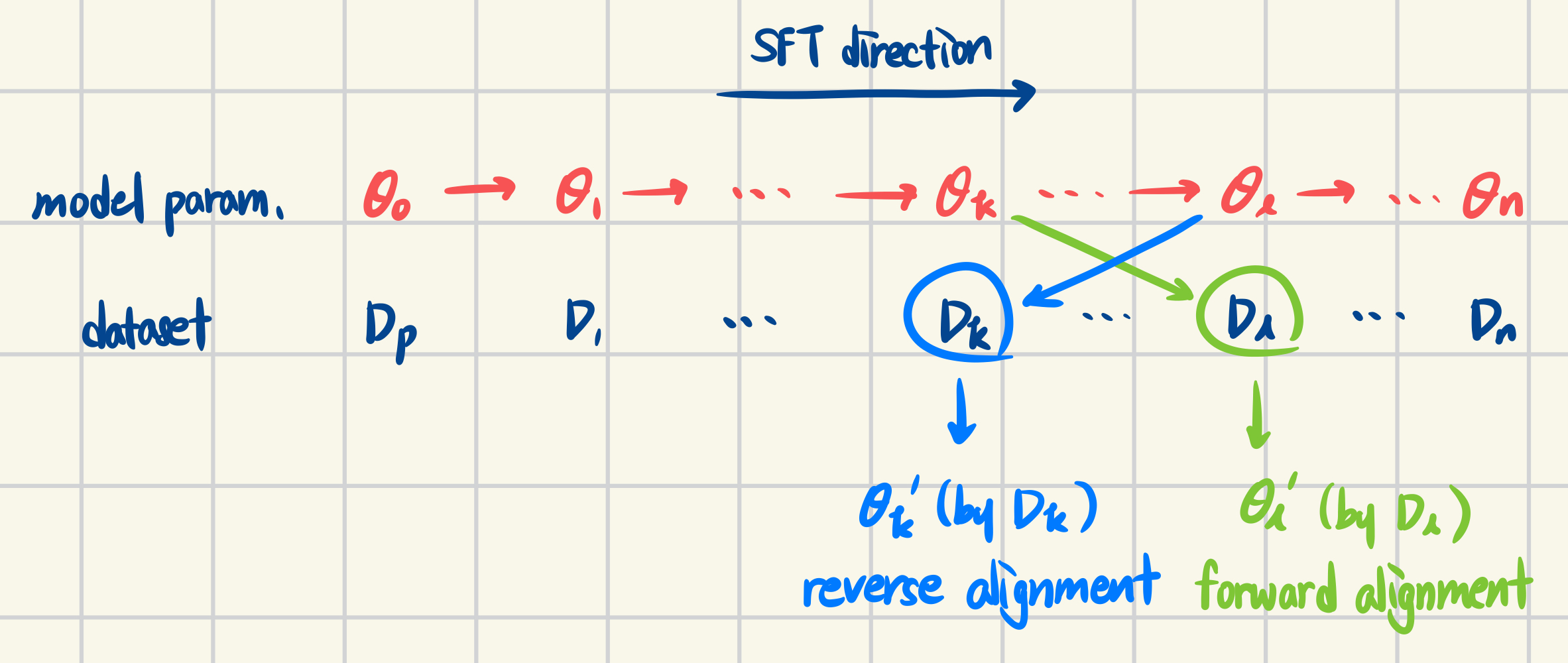
    • $\theta_0$: 사전 학습된 모델의 파라미터
    • $\mathcal{D} = \lbrace \mathcal{D}_1, \mathcal{D}_2, …, \mathcal{D}_n \rbrace$: fine-tuning을 위한 데이터셋들
    • $\lbrace \theta_1, \theta_2, …, \theta_n \rbrace$: 데이터셋 $\mathcal{D}$ 각각으로 학습 후 저장한 모델 파라미터들
    • $\theta’_k$: $\theta_k$ 모델에 대해서 이후에 학습될 데이터셋 $\mathcal{D}_l$ 을 사용하여 순방향으로 fine-tuning한 모델
    • $\theta’_l$: $\theta_l$ 모델에 대허서 이전에 학습된 데이터셋 $\mathcal{D}_k$을 사용하여 역방향으로 fine-tuning한 모델
  • 실험 설정
    • 모델의 3H (Helpful, Honest, Harmless)를 만족하는 데이터셋: Alpaca, TruthfulQA, Beavertails
    • 각 데이터셋을 $\lbrace \theta_1, \theta_2, \theta_3 \rbrace$ 로 구분
    • 모델: Llama2-7B, Llama2-13B, Llama3-8B

      하나의 데이터셋 내에서 subset으로 구분하여 역학습을 수행하는 경우가 실제로 얼마나 있는지 모르겠음
      모델의 종류와 크기가 제한되었다고 느껴짐

  • 실험 결과
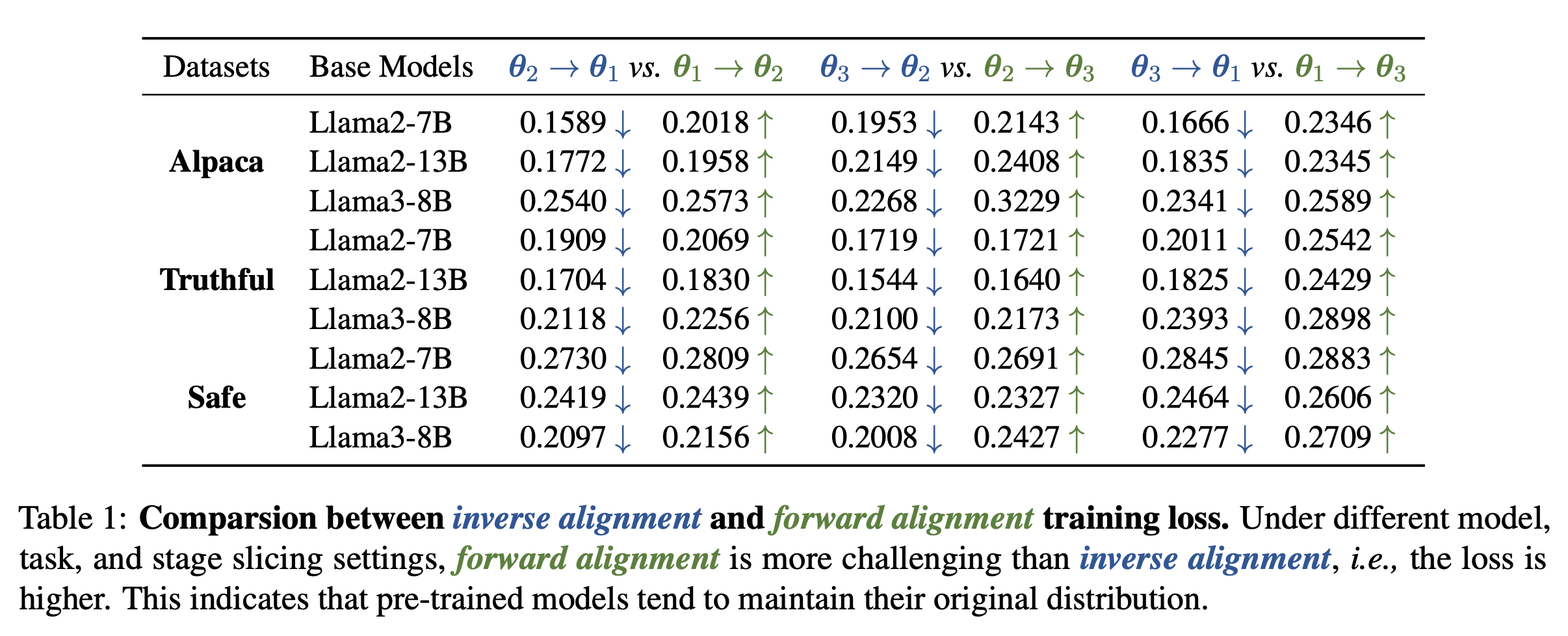
    • forward와 inverse alignment를 train loss를 통해 증명
    • 모든 경우에서 inverse alignment의 train loss가 더 낮음

      forward와 inverse alignment 과정의 train loss를 보는 것만으로 resistance를 증명할 수 있는지 모르겠음
      데이터셋 분포와 align하지 않으려는 것을 증명해야 되는데, 단순히 학습 과정이 어렵다는 것만 train loss를 통해 기록한 느낌

[ Existence of Rebound ]

  • 실험 설계
    • forward alignment에서 positive로 학습되었을 수록 inverse alignment에서는 negative로 학습되는 것을 통해 rebound를 증명
    • 두 개의 반대되는 특징(e.g., safe vs. unsafe)을 가진 데이터를 활용
    • 사전 학습 모델의 파라미터 $\theta_0$ 을 positive 데이터의 크기에 따라 학습한 파라미터 $\lbrace \theta_1, \theta_2, …, \theta_n \rbrace$ 저장
    • negative 데이터를 사용해서 inverse fine-tuning을 수행
  • 실험 설정
    • IMDb dataset: 레이블링이 되어있는 영화 리뷰 감성 분석 데이터셋으로, postivie generation을 평가
    • Beavertails: safe/unsafe 레이블링이 되어있는 QA 데이터셋으로, single-turn safe dialogue를 평가
    • positive 샘플 크기는 {1000, 2000, 5000, 10000}으로, negative 샘플 크기는 {100, 200, 500, 1000, 2000} 으로 설정

      서로 다른 레이블이 섞여있는 데이터셋의 이유는 (특히 Beavertails와 같은 경우) 무엇이 safe(긍정)이고 unsafe(부정)인지 알려주김 위함이라고 생각함.
      해당 실험 설정은 그러한 기준을 무시하고 학습을 실험한 것 같음.
      즉, 현실 세계에 실제로 모델을 적용하는 상황을 고려하여, 오히려 긍부정을 섞어서 학습한 이후에 특정 레이블에 편향된 데이터로 학습했을 때도 rebound의 특징이 나타나는지, robust하게 만들 여지가 있는지를 알려주면 좋았을 것.

    • IMDb에 대해서는 the Sentiment Roberta model을, Beavertails에 대해서는 the cost model을 사용

      여기서도, language model의 특징을 검증하려면 레이블 자체뿐만 아니라 답변의 품질을 전반적으로 평가해야 된다고 생각함.
      앞서 모델의 성능을 압축률로 표현할 수 있다고 했는데, 이는 단순히 레이블(pos/neg or safe/unsafe)에 대한 평가가 아니라 모델의 전체적인 분포와 데이터셋의 분포를 동치로 둔 것이기 때문에 어느정도의 괴리가 있는 것이 아닐까 하는 의문이 들었음.

    • 모델: Llama2-7B, Gemma-2B

      모델의 종류는 Resistance 실험 때와 왜 다른지, 그 크기가 왜 이 정도로 제한되었는지, 왜 최신 모델 대신 해당 모델들을 선택했는지 궁금함

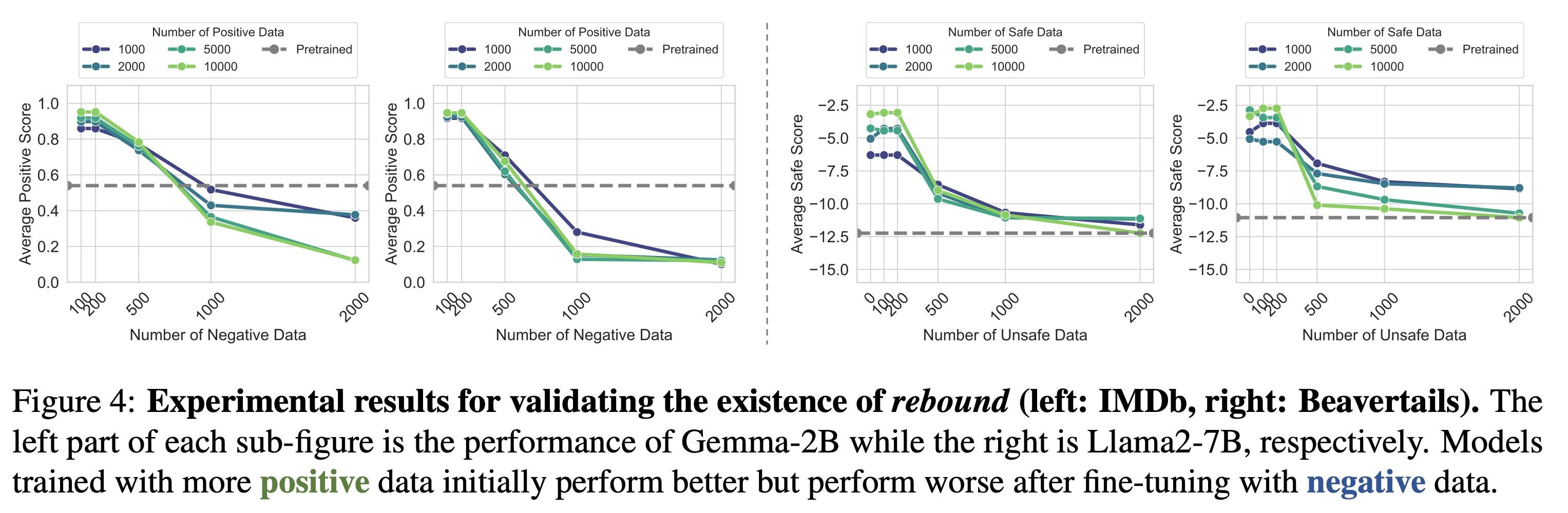
  • 실험 결과
    • 더 많은 양의 positive 데이터로 학습한 모델의 경우, inverse fine-tuning을 수행했을 때 더 빠른 감소율을 보임
    • negative 데이터의 양이 많아질 수록 pre-trained 성능으로 수렴하는 모습 → 이것은 모델이 negative 데이터셋으로 fine-tuning 하려고 시도할 때의 resistance로 볼 수 있음

      rebound에서 실험하는 reverse fine-tuning과 resistance를 실험했던 reverse alignment의 전제 조건이 다른데 이를 동치로 봐도 되는 충분한 근거가 있는지 궁금함
      또한, 그래프를 보면 Bearvertails는 pre-train의 수준으로 수렴하는데, IMDb는 pre-traindml 수준을 지나 더 낮은 점수를 기록하는 모습임. 이러한 차이가 발생하는 이유는? 왜 sentiment 분석에서 negative 데이터의 영향을 더 많이 받는지?
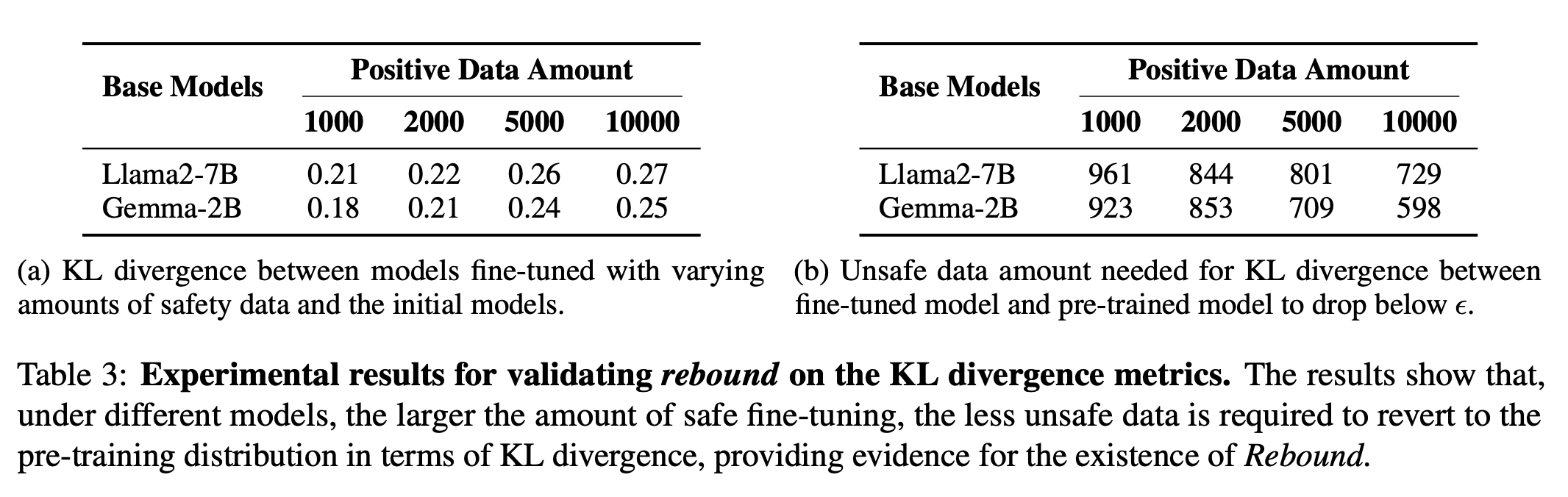
      IMDb dataset에 대해 실험한 결과를 보면 pre-trained 모델이 중립을 유지하고, Beavertails 실험 결과에서는 pre-trained 모델이 음의 점수를 기록하고 있음. 이는 base model의 성능 자체가 떨어지는 상태가 아닌지, 왜 해당 모델들을 선정한 것인지 궁금함.

    • alignment 알고리즘(RLHF, DPO, KTO, SimPO), 평가 메트릭(학습 전후의 모델 분포에 대한 KL divergence), fine-tuning 목적에 따른 rebound의 일반화가 Appendix B.2에 있음

      KL divergence를 보는 게 모델 기반의 평가보다 나았을 것 같은데 appendix로 미뤄둔 이유가 궁금함

[ Internal Factor of Rebound ]

  • 해당 파트에서 모델의 rebound에 영향을 주는 요인들을 추가로 탐색 (상세한 실험 내용은 Appendix B.3)

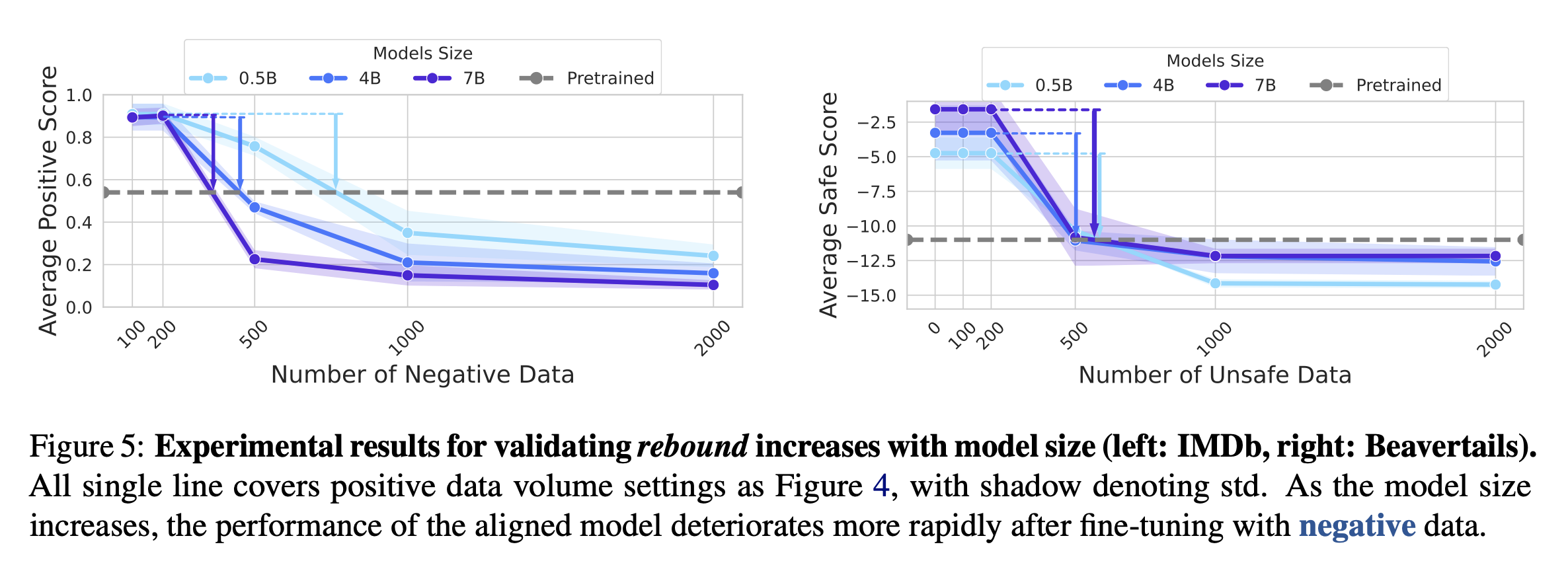
Rebound Increases with Model Size

  • Qwen 1.5 0.5B, 4B, 7B 선정
  • 모델의 크기가 클수록 rebound 비율이 큼 → 모델의 크기와 elasticity의 비례 관계

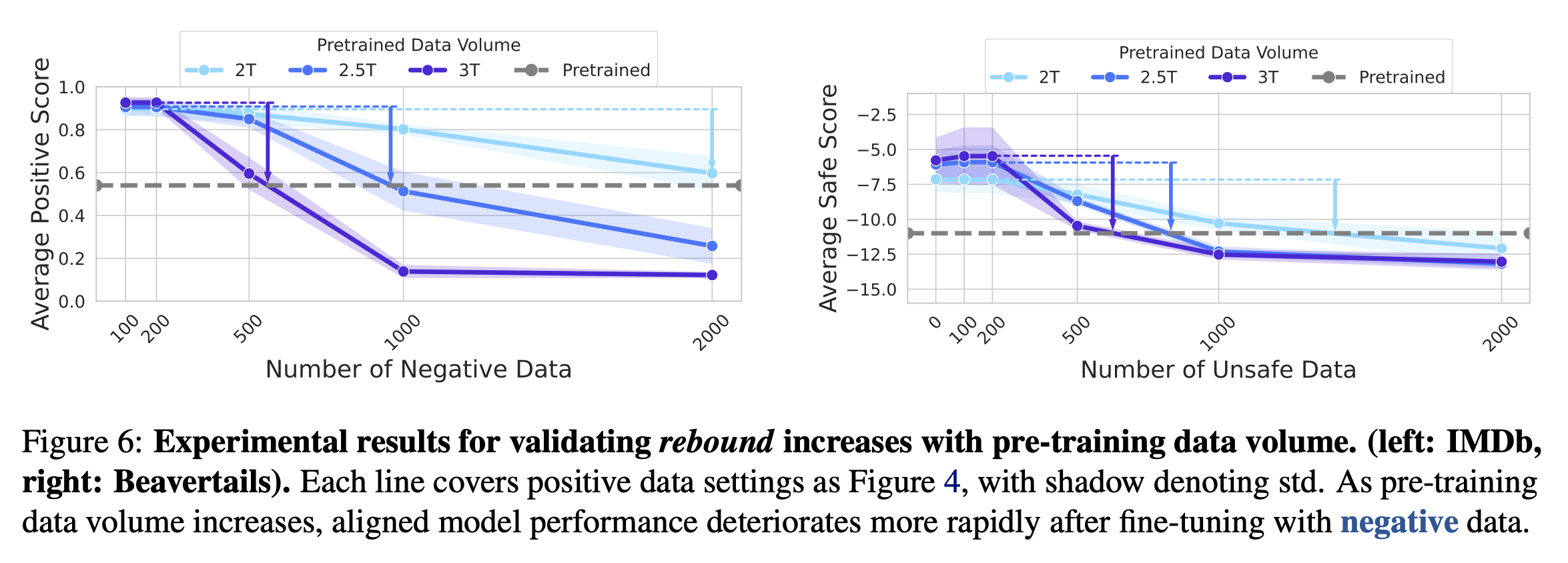
Rebound Increases with Pre-training Data Volume

  • TinyLlama에서 공개한 사전 학습 데이터셋을 2.0T, 2.5T, 3.0T로 구분하여 모델의 rebound를 실험
  • 사전 학습 데이터셋의 크기가 클수록 모델의 rebound 속도가 빠름 → 사전 학습 데이터셋의 크기와 elasticity의 비례 관계 (Theorem 4.2)

Conclusion and Outlook

[ Limitations ]

  • 한계
    • 이론적으로는 Assumption A.7(Appendix A에 가정과 증명들이 있음)의 Pareto의 mass distribution에 제한되어 있음
    • 실험적으로는 비용으로 인해 모델의 사전 학습의 전반적인 과정에 대한 elasticity를 실험하지 못한 것
  • further
    • 멀티모달 모델과 같이 언어 모델에 국한되지 않고 elasticity가 적용되는 사항인지 살펴볼 것
    • 이론적으로 모델의 elasticity와 scaling law의 관계를 살펴볼 것

[ Broader Impacts ]
Rethinking Fine-Tuning and Model Weight from Resist Alignment

  • 현재 사용되는 alignment 방식들의 한계: 현재 사용되는 방식들은 모델의 elasticity를 고려하지 못한 피상적인 방식일 뿐임
  • inverse alignment에 대한 위험성
    • elasticity로 인해 safety를 고려하여 align된 모델이라도 쉽게 이전 상태로 되돌아갈 수 있는 위험이 존재
    • Deceptive Adversarial Alignment나 Alignment Faking의 위험이 있음
  • robust한 alignment의 필요성
    • 훈련 데이터 정제는 비용이 많이 들고 효율적이지 않음
    • 단순한 피상적 변화가 아닌 파라미터 자체를 깊이 있게 수정하는 견고한 방식이 필요함

Rethinking Open-sourcing from Elasticity of LLMs

  • 오픈 소스의 양면성
    • 장점: 커뮤니티를 통해 보안 취약점 개선과 방어 전략 수립에 기여할 수 있음
    • 단점: malicious fine-tuning이나 jailbreaking에 취약할 수 있음

      jailbreaking은 closed source도 마찬가지 아님..?
      sovereign AI 강조하냐고 ㅜㅜ

  • inverse alignmen로 인한 보안 위협성
    • inverse alignment 기술이 발전하면 안전하게 alignment된 모델들이라도 위협받을 수 있음
    • jailbreaking의 장벽을 낮추고 오픈 소스 생태계의 공격-방어 균형을 무너뜨리게 됨
  • untunable alignment의 필요성
    • 모델의 elasticity 메커니즘을 이해하고 fine-tuning에 영향이 없는 untunable alignment 방식을 개발해야 함
    • 결과적으로, 모델의 전체 수명 주기 동안의 안정성을 보장해야 함

Comment

  • 너무 열심히, 특히 증명 부분은 어렵지만 재미있게 읽어서 실험 부분에 대해서 든 의문에 대해 이메일을 보내볼까 고민중이다…

의의와 강점

[ 언어 모델의 misalignment를 수식적으로 유도하고 증명함 ]

  • 모델의 misalignment를 단순히 벤치마크 성능 점수로 파악하는 것이 아니라, compression rate를 활용해서 모델의 성능에 대한 수식적 증명을 수행하여 보다 효과적으로 설명함
  • 여러 모델을 선정했을 뿐만 아니라 모델의 크기, 사전 학습 데이터셋의 크기, post training 방식 등에 따라 misalignment에 영향을 주는 요인들을 세세하게 분석함

[ AI Safety의 관점에서 우려되는 점과 지향해야 하는 바를 명확히 시사함 ]

  • 모델의 성능과 활용도가 강조되고 있는 현대에 tuning을 통해 모델에서 발생할 수 있는 우려점들을 시사함
  • 본 연구의 한계(데이터 혼합 특성, 비용 제약)와 향후 과제(OOD 데이터에서의 탄성 검증, 스케일링 법칙과의 정량적 연결, 멀티모달 확장)를 스스로 명시하였으며, 이론적 가정(토큰 트리, 모델 규모-깊이 단조성)에 대해 후속 검증을 요청하는 구도가 투명함

의문점

[ 수식적으로 설명한 내용과 실험의 alignment가 부족함 ]

  • 모델의 성능과 compression rate가 동치이기 때문에 실험에서 eval metric으로 compression rate를 사용하지 않았으나, sentiment 점수나 safety score를 측정하는 등 모델 답변의 유용성은 측정하지 않음 → 결과적으로 safety score의 비교만으로 모델의 분포가 fine-tuning 이전과 동일하다고 할 수 있는 것인지 궁금함(Appendix에서 KL Divergence에 대한 언급이 있지만, 압축률과 동등한지에 대한 설명은 부족함)

[ 실험 상황 가정이 현실적이지 않음 ]

  • resistance: 동일한 데이터셋의 데이터를 3등분해서 forward/reverse alignment를 측정했으나, 실제 환경에서 동일한 데이터셋을 사용하여 reverse alignment를 시도하는 경우는 적을 것이라고 생각됨
  • rebound: resistance와 동일하게 하나의 데이터셋 내에서 pos/neg와 safe/unsafe의 레이블을 나누어 실험했는데, 해당 학습 방식은 편향된 fine-tuning 방식인 것으로 생각되며, 현실적으로 특정 목적으로 fine-tuning된 모델에 대해 jailbreaking을 시도할 때 동일한 형태의 레이블만 반대로된 데이터를 활용할 수 있는 상황이 많지 않을 것 같음
  • 결과적으로 동일하지 않은 데이터셋을 사용했을 때 즉, fine-tuning 이후에 뒤따르는 tuning을 통해 모델의 성능이 저하되는지, 사후 분포가 pre-trained 모델의 분포로 수렴하는지 궁금함
Papers
LM Data Compression
This post is licensed under CC BY 4.0 by the author.